DM mathématiques Fonction inverse

Bonjour! Mon professeur à donné un devoir à rendre et je n'y arrive pas. J'aurais besoin d'un peu d'aide s'il vous plaît.
Voici l'énoncé:
Soit f la fonction definie sur l'intervalle ]-infini;0[ u ]0;+infini[ par f(x)=1/x et C sa courbe representative.
Soit M un point de C d'abscisse a et T la tangente a C en M.
T coupe l'axe des ordonnées en A et l'axe des abscisses en B.
Montrer que M est le milieu de [AB]

J'ai trouver ceci pour le début mais je ne suis pas sûr que cela soit bon:
Il faudrait que j'utilise cette propriété: Si A et B Sont symétrique par rapport a M alors M est le milieu du segment [AB].
Il faudrait ensuite que je montre que A et B Sont symétrique par rapport a M.
Et c'est ici que je suis bloquée!

J'attends votre réponse avec impatience

Bonjour Moi313,

Détermine l'équation de la tangente à la courbe en un point M d'abscisses $x_0$ .
$y =f'(x_0)(x-x_0)+f(x_0)$

Puis les coordonnées des points A, B et M.
Puis tu vérifies que le point M est le milieu du segment [AB].

Moi313 bonjour et bonjour Noemi,

Moi313, Noemi t'a donné tout le nécessaire.
J'espère que tu en as fait bon usage.

Je te joins un schéma

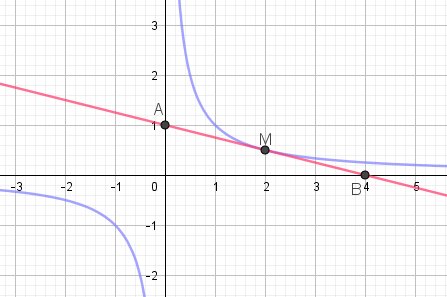
L'hyperbole est en bleu et la tangente au point M en rouge

Pour pouvoir vérifier , je t'indique des réponses

Equation de (T) : $y=−1a2(x−a)+1ay=-\frac{1}{a^2}(x-a)+\frac{1}{a}$

M a pour coordonnées $M(a,1aM(a,\frac{1}{a}$ )

Pour trouver les coordonnées de A, tu remplaces x par 0 dans l'équation de (T) et tu déduis y
Tu dois trouver , sauf erreur, $A(0,2a)A(0,\frac{2}{a})$

Pour trouver les coordonnées de B, tu remplaces y par 0 dans l'équation de (T) et tu déduis x
Tu dois trouver , sauf erreur, $B (2 a, 0)$

Ensuite, avec les formules du milieu, tu prouves que M est le milieu e [AB]

Tiens nous au courant si tu n'y arrives pas.

D'accord merci beaucoup je vais essayer et je vous dirai si j'ai réussi!

@mtschoon @Noemi
J'ai réussi a faire mon DM grace a vous! Merci beaucoup pour votre aide!

C'est bien, Moi313 !
Bon travail.