Exercice Chap.Étude de fonctions

Bonjour,
J'ai un exercice en maths que je dois faire mais ne le comprend pas j'ai fait un shema pour m aider mais sa ne m'aide pas vraiment. Voici l'exercice:

Camille vient de se fâcher avec Dominique, l'amour de sa vie! Camille l'abandonne dans un port, prend une barque et rame vers le large.
Dominique monte le plus haut possible sur les immeubles du port afin que son regard aperçoive Camille à l'horizon.
On note x l'altitude (en m) de ses yeux humides et f(x) la distance (en m) au bout de laquelle Camille disparaît à l'horizon.

1. montrer que :
F(x) = √[(6 400 000 + x)^2 - 6 400 000^2]
la racine enveloppe tous
2. Simplifier f(x).
3. Montrer que la fonction F est croissante.
4. À quelle hauteur doit monter Camille pour aperçoivoir Dominique jusqu'à une distance de 30 kilomètres ?

Voila je ne cherche pas vraiment les réponses juste comprendre.
Merci d'avance

Bonjour Massymb (et bonne année !)

Un schema devrait pourtant t"aider.
Je t'en joins un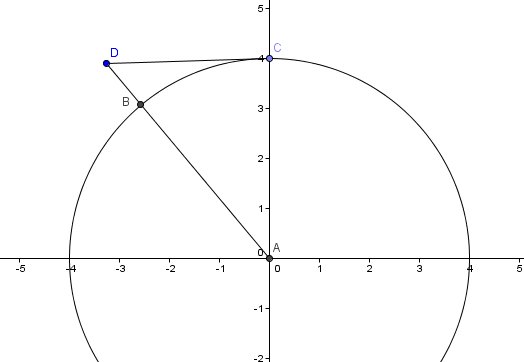

Le cercle représente la Terre de rayon R=6400000m et de centre A
Dominique est en D
Camille est en C
BD=x
DC=f(x)

Je n'ai pas fait les calculs, mais avec le théorème de Pythagore dans le triangle ADC rectangle en C, tu devrais trouver [f(x)]², puis f(x) en prenant la racine carrée.

Tiens nous au courant.

@mtschoon
Bonne année à vous aussi.
Je vais suivre votre raisonnement je vous tien au courant

Je trouve en faisant le théorème de Pythagore :
CD =(AB + x)^2 + CA^2
CD = (6 400 000 + x)^2 + 6 400 000^2
CD = √[(6 400 00 + x)^2 + 6 400 000]
C'est ce que je trouve mais dans l'énoncé c'est un - pas un + je ne comprends pas

Bonjour Massymb,

Tu as fait une erreur dans l'écriture de la relation de Pythagore ;
c'est : $AD^2 = AC^2+CD^2$
d'ou $C D = . . .$

(Bonjour Noemi et bonne année 2019)

@Massymb ,

Comme te l'a dit Noemi, il faut écrire la formule de Pythagore correctement (avec des carrés partout).
Pour réduire l'écriture, en appelant R le rayon de la terre

$AD^2=AC^2+CD)^2$
$R+x)^2=R^2+[f(x)]^2$

Tu ne dois pas avoir de difficultés pour terminer le calcul.

J'ai refait je trouve pareil que l'énoncé nickel merci

C'est bien.
Peut-être que tu n'auras pas de difficultés pour la suite, sinon reposte.

Je fait le reste et je vous tien au courant

Bonsoir @Noemi @mtschoon
Alors pour la question 2 quand je simplifie je trouve f(x)= x^2+12 800 000 donc j'en déduis pour la question 3 que la fonction et croissante vu que la fonction et une fonction carré mais je n'ais pas compris comment le montrer .
Avec un tableau de variation?

@Massymb

Je ne comprends pas l'expression de f(x) que tu donnes.
Vérifie.

J'appelle R la valeur 6 400 000

$f(x)=(R+x)2−R2=R2+x2+2Rx−R2f(x)=\sqrt{(R+x)^2-R^2}=\sqrt{R^2+x^2+2Rx-R^2}$

Donc $f(x)=x2+2Rxf(x)=\sqrt{x^2+2Rx}$

@mtschoon bonjour oui j'ai refais et je m étais trompé. Mais comment montrer que la fonction et croissante ? En faisant un tableau de variation ?

En remplaçanr R par sa valeur :
$f(x)=x2+12800000xf(x)=\sqrt{x^2+12 800 000x}$

Pour prouver que la fonction est croissante, pour x positif, tout dépend de ton cours.

Tu peux calculer la dérivée et son signe, si tu connais
ou bien utiliser le sens de variation connu des fonctions usuelles
ou bien prouver que , pour a et b positifs, a< b => f(a) < f(b)

@mtschoon d'accord merci

@mtschoon voila ce que je trouve
f(x)=x^2+12 800 000x
• a < b et f(a) < f(b)
• a^2+12 800 000a < b^2+12 800 000b
• Donc f(a) et bien < que f(b)
La fonction et croissante.
Mais je ne suis pas sûr.

@massymb,

Comme indiqué par mtschoon
Tu dois partir de 0<a<b et démontrer que f(a) < f(b),

Bonsoir @Noemi
Voila donc je trouve en étudiant le signe de f(a) - f(b)
Que si 0<a<b
alors a-b<0 et a+b>0 donc f(a)-f(b)<0
Ducoups la fonction et strictement croissante sur [0 ; +l'infini[ mais je ne vois pas comment introduire avec ma fonction
F(x)=x^2+12 800 000x .

@massymb

A partir de 0 < $a$ < $b$
tu déduis 0 < $a^2$ < $b^2$
et 12800000 $a$ < 12800000 $b$
donc
$a^2$ + 12800000 $a$ < $b^2$ + 12800000 $b$
puis
$f (a)$ < $f (b)$

puis tu conclus.

Bonjour Massymb et Noemi,,

@Massymb
Pour la 3), Noemi ta bien détaillé le sens de variation de f

Je regarde la question 4) et je comprends guère...
Tu as écrit :
"À quelle hauteur doit monter Camille pour aperçevoir Dominique jusqu'à une distance de 30 kilomètres ?"

Au début de l'énoncé tu indique que c'est Dominique qui monte le plus haut possible (de la distance DB=x)

Alors, n'y a-t-il pas une confusion entre Camille et Dominique ?

@mtschoon bonjour oui justement c'est ce qu'il ya marqué dans l énoncer je me posais la même question que vous. Je pense qu'il ya confusion.

Effectivement, si tu n'as pas fait une erreur de copie, c'est qu'il y a une erreur dans l'énoncé de la 4)

Tu peux éventuellement, s'il s'agit d'un devoir à rendre, recopier la question en rectifier l'erreur et faire la 4) rectifiée :

f(x)=30(km) et tu cherches x

@mtschoon @Noemi d'accord merci je comprends mieux

Je ne comprends pas comment faire pour f(x)=30 et touver x

Bonsoir Massymb ,
Tu résous l'équation $x^2+12800000x = 30000^2$
soit $x^2+12800000x - 900000000 = 0$

Bonsoir @Noemi ha d'accord je m'étais trompé dans l équation merci

@massymb,

Tu as trouvé la valeur de $x$ ?

@noemi eu en faisant avec le discriminant pour trouver les racines je trouve x1= -12 800 000
Et x2= 0.00195315
Ce n'est pas normal
Sûrement une erreur

@massymb
Oui une erreur un oubli du carré dans l'écriture de l'équation.
Refais les calculs.

@Noemi voila je trouve
x1 = - 81 921 806 400 000
x2 = 81 921 806 400 000
Sa me paraît beaucoup trop

@massymb,

Vérifie tes calculs, je trouve 70,31.... et -12800070,31.

Bonjour Massymb et Noemi,

@Massymb
Je pense qu'au départ, tu n'avais pas converti les km en mètres 30km=30000m et je ne te l'avais pas indiqué .

Evidemment, vu les valeurs, il y a de quoi faire des erreurs.

Pour les valeurs approchées des solutions, je confirme les solutions de Noemi : ma calculette me renvoie les mêmes.

Bien sûr, vu que x est positif la réponse est environ 70.3121(m) que l'on peut peut-être arrondir à 70.3(m)

Bons calculs.

@Noemi @mtschoon effectivement c'était ma calculatrice qui était déréglé je les changer et je trouve pareille merci beaucoup de votre aide.

De rien ! Nous faisons au mieux.
A+