exercice math exercice 2 géométrie
-
Ssoleilla dernière édition par
Bonjour, j'ai un problème de math que je n'arrive vraiment pas à résoudre. Quelqu'un pourrait-il m'aider s'il vous plait ?
Alors c'est un triangle ABC. AB est la base. Il y a un point E sur le segment AC et un point F sur le segment CB.
Les points E et F forment un segment qui est parallèle à AB. AB mesure 5 cm. et l'énoncé dit que le triangle est découpé en 2 zones: première zone A,E,F,B (partie basse du triangle) et E,C,F (partie haute du triangle). Ces deux zones ont la même aire.Il faut trouver la longueur EF.
-
Bonsoir soleilla,
As tu fais une figure ?
Note h la hauteur du triangle CEF, h' la hauteur du trapèze EFBA et x la longueur EF.
Ecris les aires des triangles et du trapèze puis la relation de Thalès pour les triangles.
A partir des relations obtenues du détermines x.
-
mtschoon dernière édition par mtschoon

soleilla bonjour, et bonjour Noemi.
@soleilla
Comme te l'a demandé Noemi, j'espère que tu as fait une figure.
Pour plus de clarté pour les explications, j'en joins une ici :
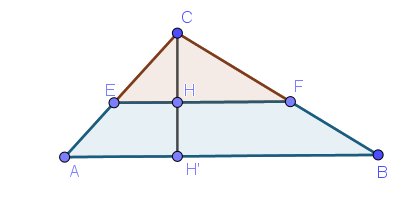
Je t'avance un peu le travail
En posant CH=h
Utilisation de la formule de l'aire d'un triangle
aire(CEF)=EF×CH2=xh2aire(CEF)=\dfrac{EF \times CH}{2}=\dfrac{x h}{2}aire(CEF)=2EF×CH=2xhEn posant HH'=h'
Utilisation de la formule de l'aire d'un trapèze
aire(AEFB)=(AB+EF)2×HH′=(5+x2)h′aire(AEFB)=\frac{(AB+EF)}{2}\times HH'=\biggl(\dfrac{5+x}{2}\biggl) h'aire(AEFB)=2(AB+EF)×HH′=(25+x)h′D'où l'égalité
xh2=(5+x2)h′\dfrac{x h}{2}=\biggl(\dfrac{5+x}{2}\biggl) h'2xh=(25+x)h′Maintenant, il te reste à utiliser le théorème de Thalès pour trouver une relation entre h et h' et faire une simplification pour trouver une équation d'inconnue x.
Tiens nous au courant si besoin.