Dérivation Tracer la tangente à une courbe à partir du nombre dérivé problème d'application
-
LLili12 dernière édition par
Bonjour !
Je n'arrive pas à tracer la tangente à une courbe à partir du nombre dérivé.
Si je veux tracer la tangente qui passe par A(-0,5 ; 6) tel que f'(-0.5)=9
Afin de tracer la tangente, si j'ai bien compris, il faut donc que j'avance horizontalement de -0.5 unité et que j'avance verticalement de 9 unités, en partant du point A?Si c'est le cas, et bien cela ne marche pas sur mon graphique

Merci d'avance !
-
Bonjour Lili12,
La pente est égale à 9, cela veut dire que si à partir du point A, tu avances horizontalement de une unité ( et non de -0,5), il faut avancer verticalement de 9 unités.
-
mtschoon dernière édition par mtschoon

Lili12 bonjour,
Le nombre dérivé 9 est le coefficient directeur de la tangente.
Je te mets un schéma et je vais essayer de te l'expliquer.
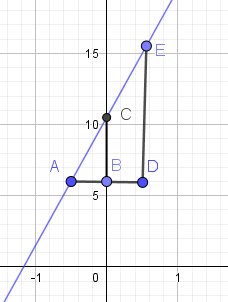
Tu places le point A(-0.5,6)
Je t'explique le raisonnement.
E étant un point que tu veux placer pour construire la tangente,
par définition du coefficient directeur d'une droite, tu dois avoir
yE−yAxE−xA=9\dfrac{y_E-y_A}{x_E-x_A}=9xE−xAyE−yA=9Le plus simple est de prendre xE−xA=+1x_E-x_A=+1xE−xA=+1
ainsi, yE−yA=+9y_E-y_A=+9yE−yA=+9Pour cela, à partir du point A, parallèlement à l'axe des abscisses et dans le sens de l'axe des abscisses, tu places le point D tel que AD=1
A partir du point D, parallèlement à l'axe des ordonnées et dans le sens de l'axe de ordonnées (vu que le nombre dérivé est positif), tu places le point E tel que AE=9
La tangente est la droite (AE)
Tu peux vérifier que cette construction satisfait bien à la définition donnée du coefficient directeur.Bien sûr, tu aurais pu, par exemple, prendre , au lieu de D, le point B tel que AB=0.5
Dans ce cas, il aurait fallu trouver un point C de la tangente tel que
yC−yAxC−xA=9\dfrac{y_C-y_A}{x_C-x_A}=9xC−xAyC−yA=9
Avec xC−xA=0.5x_C-x_A=0.5xC−xA=0.5, il faut que yC−yA=4.5y_C-y_A=4.5yC−yA=4.5
En faisant comme précédemment , tu obtiendras le point C et la tangente (AC) qui sera évidemment la même.Bonne réflexion.
Reposte si mon explication n'est pas assez claire.
-
mtschoon dernière édition par

Bonjour Noemi.
Comme je tapais une explication détaillée, je n'avais pas vu ta réponse...
-
LLili12 dernière édition par
Merci énormément pour ces explications ! J'ai tout compris.
Bonne journée.
-
C'est bien si tu as compris ton erreur.
-
mtschoon dernière édition par mtschoon

C'est parfait si tu as compris l'explication.
Evidemment, lorsque tu auras vu , en cours, l'équation d'une tangente, tu pourras aussi, avec l'équation, construire la tangente.
Bon week-end .