Fonction définie par intégrale
-
?Un Ancien Utilisateur dernière édition par mtschoon
Bonsoir tout le monde
J'ai une question concernant le domaine de définition d'une fonction définie par intégrale
Ma fonction est :
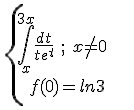
Je dois prouver que cette fonction est définie sur IR mais je me bloque dès le début car 1/(te^t) n'est pas défini en 0 .
Merci d'avance pour votre aide et soutien!!
-
mtschoon dernière édition par mtschoon

EL bonsoir,
Il y a deux cas qui définissent f
Pour x≠0x\ne 0x=0 , f(x) est l'intégrale sur l'intervalle [x,3x] qui ne contient pas la valeur 0, dont t ne prend pas la valeur 0 sur cet intervalle.
En détaillant l'explication :
Pour x>0, nécessairement 3x>0.
Sur l'intervalle [x,3x], t >0 donc t ne s'annule pas
Pour x<0, nécessairement 3x<0.
Sur l'intervalle [x,3x], t <0 donc t ne s'annule pasf est donc bien définie pour x≠0x\ne 0x=0
Pour x=0x=0x=0, par la définition donnée qui n'a rien à voir avec l'intégrale, l'énoncé pose arbitrairement f(0)=ln3
f est ainsi bien définie pour x=0Conclusion :
avec l'union des des deux cas : f est définie sur R.
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
@mtschoon
Mais la fonction 1/(te^t) n'est pas continue sur R* , voilà mon problème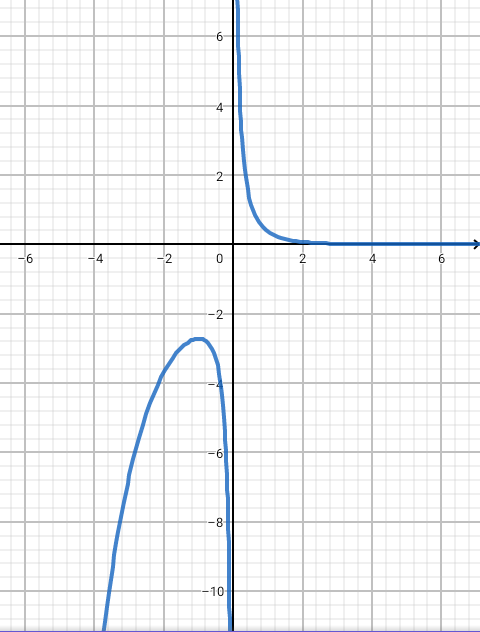
-
mtschoon dernière édition par mtschoon

@EL
Tout à fait d'accord sur le graphique de t ->1/(te^t)
Cette fonction est continue sur ]0,+∞[]0,+\infty[]0,+∞[ et sur ]−∞,0[]-\infty,0[]−∞,0[
Sur ]0,+∞[]0,+\infty[]0,+∞[ et sur ]−∞,0[]-\infty,0[]−∞,0[ , la fonction f est définie comme intégrale de bornes x et 3x
Pour 0, l'énoncé te dit que f(0)=ln3 (ce qui n'a rien à voir avec l'intégrale)Donc f est définie sur ]−∞,0[∪ ]-\infty,0[ \cup \ ]−∞,0[∪ {0} ∪]0,+∞[=R\cup ]0,+\infty[ = R∪]0,+∞[=R
-
BBlack-Jack dernière édition par
On ne demande pas que f(x) soit continue en 0, mais juste qu'elle soit définie et c'est ce cas dès que l'énoncé précise que f(0) = ln(3)
Néanmoins on peut quand même montrer que f est continue en 0, ainsi par exemple :
Ce n'est pas 1/(t.e^t) qui doit être continue mais bien S(de x*3x) dt/(t.e^t)
Le seul problème potentiel est aux alentours de 0.
développement de e^t près de 0 : 1 + t + t²/2 + ...
et donc près de 0, on a t * e^t = t + t² + t³/2 + ...
et donc aux alentours de 0, on a : t.e^t = t + 0(t²)
et donc pour x aux alentours de 0, S(de x*3x) dt/(t.e^t) presque égal à S(de x à 3x) 1/t dt = [ln|t|](de x à 3x) = ln|3x|-ln|x| = ln|3x/x| = ln(3)
Donc lim x--> 0 de S(de x*3x) dt/(t.e^t) = ln(3)
On peut donc prolonger f(x) en 0 par f(0) = ln(3)
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
Merci beaucoup @mtschoon et @Black-Jack vous m'avez beaucoup aidé à comprendre


-
mtschoon dernière édition par mtschoon

@EL
C'est parfait El si maintenant c'est clair pour toi.

Je suppose qu'il s'agit seulement de la première question de l'exercice.
Peut-être que la suite ne te posera pas de difficultés, sinon reposte .
Bon travail !
-
?Un Ancien Utilisateur dernière édition par
@mtschoon oui le reste était clair et un peu facile ... vous avez raison!