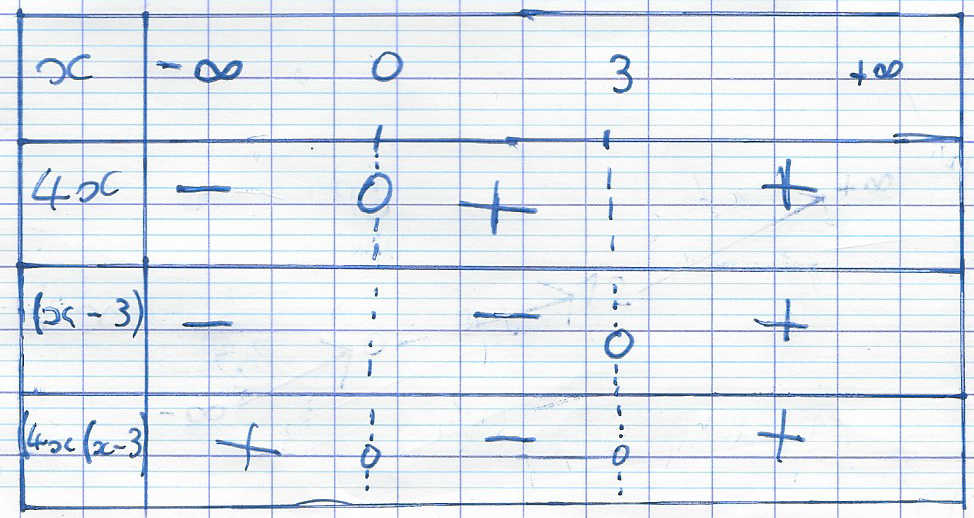polynôme du second degré (équations, inéquation)

Soit f la fonction définie sur R par f(x)=4x²-12x+5.

Montrer que, pour tout x, f(x)=(2x-5)(2x-1) et f(x)=4(x-1,5)²-4.
En utilisant la forme la plus adaptée, résoudre :
a. l'équation f(x) = -4
b. l'inéquation f(x) ≥ -4
c. l'équation f(x) = 0

Bonjour,
J'ai cet exercice à faire pour la rentrer mais je ne sais pas du tout comment faire. Pourriez-vous m'aider s'il vous plait ?
Merci d'avance

Bonjour,

Pour la question 1, c'est facile.

Tu pars de f(x) = (2x-5).(2x-1)
Tu développes le 2ème membre et, sauf erreur, tu devrais retrouver l'expression f(x) = 4x²-12x+5

Et ensuite, tu pars de f(x) = 4.(x-1,5)²-4
Tu développes le 2ème membre et, sauf erreur, tu devrais retrouver l'expression f(x) = 4x²-12x+5

Il te reste à le faire ...

Bonjour enzo,

Le scan de l'énoncé d'un exercice est interdit sur ce forum. Il va être supprimé.
Seuls les schémas et graphiques sont autorisés.
Recopie l'énoncé et indique tes éléments de réponse.

@Noemi désolé je ne le savais pas. C'est ma première utilisation du site. Je vais supprimer le scan.

@enzo , @Noemi ,@Black-Jack

Bonjour à tous,

Effectivement enzo, comme te l'a dit Noemi, les scans d'énoncés ne sont pas autorisés sur le forum et on ne doit donner de l'aide que lorsque l'énoncé est recopié.

Black-Jack ne devait pas le savoir lorsqu'il a répondu. Maintenant, il le sait.

enzo, tu n'as pas besoin de supprimer le scan car c'est déjà fait par la modération.

Ah ok merci

@Black-Jack c'est bon je l'ai fait. J'ai bien trouvé le même résultat que la première expression. merci

il me reste à faire le 2 : je sais résoudre mais je ne sais pas comment choisir la forme la plus adaptée.

@enzo

Avec l'énoncé donné :

Piste pour la 2)

f(x)=4(x-1,5)²-4 est commode pour a) $f (x) = - 4$ et b) $f(x)≥−4f(x)\ge-4$

f(x)=(2x-5)(2x-1) est commode pour la c) $f (x) = 0$

@enzo

Pour choisir la forme adaptée, tu choisis celle qui te permet d'obtenir le résultat le plus rapidement.
Pour le a : C'est la forme qui contient déjà -4 qui est à utiliser.
Je rectifie pour le b car il me semble que sur le sujet de départ c'est l'inéquation $\geq5$ donc il faut utiliser la première écriture, celle avec le 5.
Pour le c : La forme factoriser car on utilise le fait qu'un produit de facteur est nul si et seulement si .....

@enzo

A toute fin utile, je t'indique des réponses pour que tu puisses comparer aux tiennes

Avec l'énoncé donné :

a) x=1.5 pour $f (x) = - 4$
b) Tout x réel convient pour $f(x)≥−4f(x)\ge -4$
c) x=2.5 ; x=0.5 pour $f (x) = 0$

Reposte si besoin.

j'était parti en vacance mais la je m'y remet. Je ne comprend pas comment faire : à un moment il faut isoler le x de 4x² mais je n'y arrive pas.

Bonjour enzo,

Précise la question qui te pose problème. Indique tes calculs.

@Noemi
pour le 1) , j'ai fait :
4(x-1,5)²-4 = -4
4(x-1,5)² = 0
4(x²-3x+2,25) = 0
4x²-12x+9 = 0
4x²-12x = -9
4x² = -9/12

Et la je bloque.

@enzo

A partir de
$4(x-1,5)^2 = 0$
il te suffit d'écrire
$(x - 1, 5) = 0$
soit $x = . . . . .$

@enzo

Tu as fait des erreurs en fin de calcul , mais de toute façon, ce n'est pas l'idée.

$4(x-1,5)^2 = 0$ <=> $x-1.5)^2=0$ (vu que 4 est non nul)

$x-1.5)^2$ est nul si et seulement si $(x - 1.5)$ est nul, donc....

donc si je comprend bien :
4(x-1,5)²-4 = -4
4(x-1,5)² = 0
4(x-1,5)=0
4x-6=0
4x=6
x=6/4
x=1,5

@enzo

Oui
Remarque :
$4(x-1,5)^2 = 4(x-1,5)(x-1,5)$
et un produit de facteur est nul si et seulement si l'un de ses facteurs est nul
comme 4 différent de 0, il reste $(x - 1, 5) = 0$ soit $x = 1, 5$ .

ok . merci . J'ai juste une dernière question : si je met le dernier raisonnement sur ma copie, est-ce que j'ai besoin de préciser que (x−1.5)² est nul si et seulement si (x-1.5)(x−1.5) est nul ?

@enzo

Non, juste $(x - 1, 5) = 0$

ok . merci beaucoup .

Est-ce que c'est le même raisonnement pour le 2) ?

@enzo

Non puisque tu résous une inéquation.
Pars de l'écriture de $f (x)$ avec -4.
....

tu a pourtant dis plus haut dans la conversation qu'il fallait utiliser l'ecriture de f(x) avec 5.

@enzo

Cela dépend de l'énoncé : Est-ce $\geq -4$ ? ou $f(x)≥5f(x)\geq 5$ ?

pour le b, c'est f(x)≥5

@enzo

Donc tu pars de l'écriture de la fonction qui contient 5.
Tu écris sous la forme $\geq 0$
Tu factorises l'expression $A (x)$
puis tu fais un tableau de signes.

4x²-12x+5≥5
4x²-12x≥0

Et la je ne comprend pas comment on peut factoriser.

@enzo

Mets $4 x$ en facteur
$4x^2 - 12x = 4x ( ....- .... )$

4x ² −12x=4x(4x−12x)

@enzo

Non,
$4x2−12x=4x×x−4x×3=4x(.....−.....)4x^2 - 12x = 4x \times x - 4x \times 3 = 4x( ..... - .....)$

4x² −12x=4x(3x−3)

@enzo

Non,
$4x2−12x=4x×x−4x×3=4x(x−3)4x^2 - 12x = 4x \times x - 4x \times 3 = 4x( x - 3)$
Il te reste à résoudre $\geq 0$

sa revient a faire 4x²-12x puisqu'il faut développer pour résoudre.

@enzo

Non, tu fais un tableau de signes :
$x$ $−∞-\infty$ 0 3 $∞\infty$
$4 x$
$x - 3$
$4 x (x - 3)$

J'ai pas compris le truc du tableau de signe.

@enzo

Tu n'as pas vu les tableaux de signes en cours ?

Pour $4 x$ c'est - 0 +

C'est comme ça ?

@enzo

Non,

ça c'est un tableau de variations. Mais tu peux voir avec ces variations que $4 x$ est négatif si x < 0 et 4x est positif si x > 0.

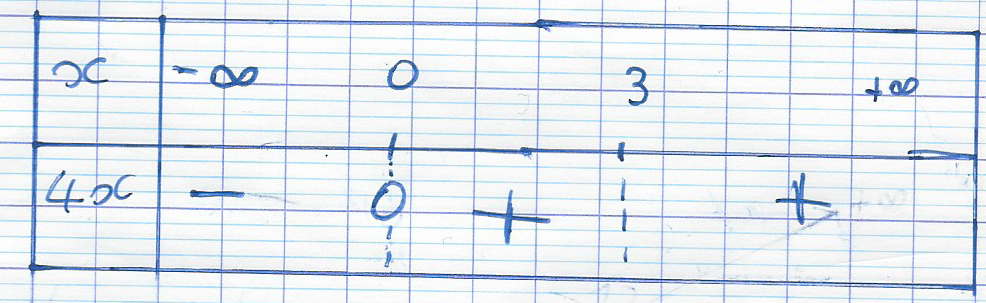
@enzo

Oui
rajoute les lignes
$(x - 3)$
et le bilan
$4 x (x - 3)$

@Noemi

enzo , bonjour,

Ton dernier tableau de signes est bon.

Tu en déduis l'ensemble des solutions de l'inéquation 4x²-12x≥0

@mtschoon
ben du coup, c'est ]−∞;+∞[
non ?

@enzo

Supérieur ou égal à 0 correspond aux intervalles ou tu as obtenu le signe + .

@Noemi
Alors c'est ]-∞;0[U]0;+∞[ ou ]-∞;0[U]3;+∞[ ?

@enzo

Regarde bien le tableau

"+" correspond à la première colonne et à la 3ème colonne

Regarde le haut de ces deux colonnes

Pour la première colonne, x est entre $−∞-\infty$ et 0
Pour la troisième colonne, x est entre 3 est $+∞+\infty$

Donc les solutions de l'inéquation sont les réels de
$]−∞]-\infty$ ,.....]U[......,, $+∞+\infty$ [

Tu complètes.

@Noemi Alors ]-∞;0[U]3;+∞[ ?

@enzo
C'est : ]-∞;0]U[3;+∞[
L'inégalité n'est pas stricte, tu prends aussi les cas ou c'est égal à 0, donc pour $x = 0$ et pour $x = 3$ .