Division euclidienne (a=bq+r ; 0=<r <b)

Bonsoir tout le monde
J'ai une question concernant l'arithmétique
Soit a=n^3-n+5 et b=n-3
Trouvez q et r tel que a=bq+r et
0=<r <b
La seule idée que j'ai est de faire la division euclidienne mais je trouve r que r n'est pas encadré entre 0 et b
Mercii d'avance! !!

Bonsoir EL,

Indique tes éléments de réponse.

D'accord @Noemi
q = n^2+3n+8
r = 29

@EL

Avec cet énoncé, tes calculs sont justes.

@Noemi mais r doit être encadré entre 0 et b ! (Pour tous n appartenant à N*)
Alors que dans ce cas on a 29 <n-3 (ça veut dire que n doit être supérieur à 32 !)

@EL

Exact, mais au départ b > 0 et b = n-3 donc n > 3.

Y a t-il d'autres questions à cet exercice ?

@Noemi non c'est la seule question et aussi b n'est pas supérieur à 0 car il peut appartenir à Z en cas de n=1 ou 2

Bonjour EL et Bonjour Noemi,

Je jette un coup d'oeil sur cette question.

@EL
Je suppose qu'il s'agit de la division euclidienne dans N, vu que tu écris dans le titre a=bq+r avec $0≤r<b0\le r \lt b$
(si c'était dans Z, ce serait a=bq+r avec $0≤r<∣b∣0\le r \lt|b|$ )

Pour n > 3, b est strictement positif et a est bien positif (tu peux le vérifier).

$q = n^2+3n+8$ et $r = 29$ sont bien les bonnes réponses pour la division euclidienne, mais comme tu l'as indiqué, seulement pour $n>32n\gt 32$

En appliquant ces formules pour $3<n≤323\lt n \le 32$ , la transformation donnée ne correspond plus à la division euclidienne indiquée.

Si la division euclidienne est bien la question (?), pour $3<n≤323\lt n \le 32$ , il faut que tu fasses les autres cas.

Evidemment, avec un tableur, les calculs se font tous seuls.
A toute fin utile, je t'indique un tableau fait avec Excel (en utilisant ENT pour le quotient entier et MODE pour le reste)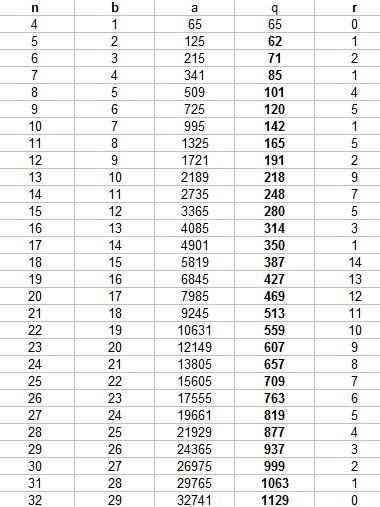

Vérifie tout de même ton énoncé.

@mtschoon merci beaucoup! J'ai pas pensé à faire tout ces calculs

De rien EL
c'est une solution possible.

Bonsoir!
Je veux seulement partager avec vous la méthode que mon prof a utiliser pour résoudre se problème;
On a:
n^3-n^2+6=(n-3)×(n^2+2n+6)+23

E(23/(n-3))=0 ==> r=23
E(23/(n-3))=1 ==> r=23-(n-3)×1=26-n
E(23/(n-3))=2 ==> r=23-(n-3)×2 =29-2n
En général :
E(23/(n-3))=k ==> r=23-(n-3)×k
pour 0 =< k =< 23

Bonjour EL,

Merci EL pour le partage. Cette méthode est intéressante.

Il y a tout de même des choses bizarres.

Dans la première version, il s’agissait de la division euclidienne de $n^3-n+5$ par $n - 3$
Dans la seconde version que tu indiques ici, le dividende est différent : il s’agit de $n^3-n^2+6$

Il n’est peut-être question ici que d’un exemple pour expliquer la démarche, qui n'a rien à voir avec la première version ... ?

La deuxième version commence par :
$n3−n2+6=(n−3)×(n2+2n+6)+23n^3-n^2+6=(n-3)\times (n^2+2n+6)+23$

Ne serait-ce pas plutôt $n3−n2+6=(n−3)×(n2+2n+6)+24n^3-n^2+6=(n-3)\times (n^2+2n+6)+24$ ?

La discussion devrait être ensuite basée sur $E(24n−3)E\biggl(\dfrac{24}{n-3}\biggl)$

Merci de vérifier.

Bonjour,

1 ère version d'énoncé.

En faisant la division euclidienne de n³-n+5 par (n-3), on trouve :

n³-n+5 = (n-3).(n²+3n+8) + 29

Mais il faudrait encore que 29 < n-3 --> seulement valable pour n > 32

Si n < 32 :

n³-n+5 = (n-3).(n²+3n+8 + k) + 29 - k(n-3)

On a alors q = (n²+3n+8 + k) et r = 29 - k(n-3) ... avec la condition sur k que : 29 - k(n-3) < (n-3)

donc que k > (32-n)/(n-3), il faut prendre k entier le plus petit possible mais respectant la condition ci-avant.

Et si n = 32,alors r = 0 et q = 1129

Groupement des résultats :

Si n = 32 : r = 0 et q = 1129
Si n > 32 : r = 29 et q = n²+3n+8
Si n < 32 : r = 29 - k(n-3) et q = (n²+3n+8 + k) avec k le plus petit entier > (32-n)/(n-3)

Ex numériques pour vérifications :

1°)

n = 22 (donc < 32)
n³ - n + 5 = 10631

(n-3) = 19
k >= (32-n)/(n-3) (entier le plus petit possible) ---> k >= 0,52 ---> prendre k = 1

q = (n²+3n+8 + k) = 559
r = 29 - k(n-3) = 10

10631 = 559 * 19 + 10

2°)

n = 5 (donc < 32)

n³ - n + 5 = 125

(n-3) = 2
k >= (32-n)/(n-3) (entier le plus petit possible) ---> k >= 13,5 ---> pendre k = 14

q = (n²+3n+8 + k) = 62
r = 29 - k(n-3) = 1

125 = 62 * 2 + 1

3°)

n = 50 --> > 32 et alors on doit faire : n³-n+5 = (n-3).(n²+3n+8) + 29

n³ - n + 5 = 124955
q = n²+3n+8 = 2658
r = 29

124955 = 2658*47 + 29

Re bonjour EL,

Pour la "seconde version", tu as peut-être fait une faute de frappe en donnant l'expression.

Si le dividende était $n^3-n^2+5$ , ton explication serait bonne
$\fbox{n^3-n^2+5=(n-3)(n^2+2n+6)+23}$

Ce que tu indiques n’est sans doute qu’une ébauche car en changeant le reste à chaque étape, comme c’est le cas dans cette méthode, le quotient change à chaque étape.
Il faut donc aussi étudier le quotient associé.
Supprimer (n-3) au reste, revient, pour équilibrer la formule, à ajouter 1 au quotient.
La formule générale du quotient doit être : $\fbox{q=n^2+2n+6+k}$

Effectivement, dans une division euclidienne dans N de la forme A=BQ+R la condition $0≤R<B0\le R\lt B$ peut s’exprimer en partie entière :
$0≤R<B0\le R\lt B$ <=> $\le \dfrac{R}{B} \lt 1$ <=> $E(RB)=0E\biggl(\dfrac{R}{B}\biggl)=0$

Je regarde les lignes que tu indiques.

Première ligne : $E(23n−3)=0E\biggl(\dfrac{23}{n-3}\biggl)=0$ correspond à $0≤23<n−30\le 23\lt n-3$
C'est le cas « standard » où la division euclidienne dans N indiquée s'applique, avec $q=n^2+2n+6$ et $r = 23$ , pour $\fbox{n \gt 26}$

Les autres lignes permettent de dégager une formule littérale plutôt que de faire des calculs numériques pour $\fbox{3 \lt n \le 26}$.

Seconde ligne : : $E(23n−3)=1E\biggl(\dfrac{23}{n-3}\biggl)=1$ correspond à $E(23−(n−3)n−3)=0.E\biggl(\dfrac{23-(n-3)}{n-3}\biggl)=0.$
Elle correspond $0≤23−(n−3)<n−30\le 23-(n-3)\lt n-3$
Dans ce cas, $q=n^2+2n+6+1=n^2+2n+7$ et $r = 23 - (n - 3) = 26 - n$
Ce serait bien, il me semble, d’expliciter les valeurs de n concernées.
Sauf erreur , ce cas correspond à $15≤n≤2615\le n \le 26$

Même idée pour les lignes suivantes, mais évidemment, expliciter n ne simplifie pas la tâche, mais cela me semble utile.

Cette étude est très intéressante et je t’en remercie.

Bon travail !

PS : ne te fais pas de soucis pour ce changement de pseudo sur ce topic, c'est un bug informatique.

Bonjour,

Si on désire généraliser ... c'est sans difficulté.

Avec n³-n²+5 à diviser par (n-3)

Pour tout n > 3, on trouve :

q = n² + 2n + 7 + E((26-n)/(n-3))
et
r = 26 - n - (n-3) * E((26-n)/(n-3))