Fonction avec partie entière - Limites

[hafud]

Bonsoir pouvez vous m'aider à trouver les solutions de cette exercice
On considère la fonction f défini par
f(x)=xE(2/x)
1)a) montrer que quelque soit x>0
2-x<f(x)≤2
b) calculer $limf(x)$ en 0 si x>0
c) est ce que la fonction ait une limite en point $a=0$
2) écrire l'expression du fonction $f$ sur l'intervalle ]2;+∞[ puis déduire $limf(x)$ en +∞
3) montrer que $limf(x)$=+∞ en -∞

[Noemi]

Bonsoir hafud,

Indique tes éléments de réponse et la question qui te pose problème.
Analyse $E(2/x)$ .

[mtschoon]

Bonjour hafud et bonjour Noemi,

Piste pour démarrer,

Propriété utile de la partie entière :

Pour tout X réel, $\fbox{E(X)\le X\lt E(X)+1}$
Vu la question posée, hafud, cette propriété doit faire partie de ton cours.

Pour $X=\frac{2}{x}$ :

$E\left(\frac{2}{x}\right)\le \frac{2}{x}<E\left(\frac{2}{x}\right)+1$

En multipliant par x, pour x>0 (donc sans changer le sens des inégalités) :

$xE\left(\frac{2}{x}\right)\le 2<xE\left(\frac{2}{x}\right)+x$

c'est à dire : $\fbox{f(x)\le 2\lt f(x)+x}$

La réponse à la question 1)a) est ainsi immédiate.

$\fbox{2-x\lt f(x)\le2}$

La question 1)b) en est la conséquence directe.

[hafud]

@mtschoon pour c

[mtschoon]

@hafud
Merci de commencer à indiquer ce que tu as trouvé comme limite en 0 à droite (x > 0) (question 1)b)) avant de paaser à la 1)c) .

[mtschoon]

Bonjour,

hafud a dû terminer vu qu'il n'a pas donné suite

Quelques pistes , pour consultation éventuelle.

1)b) : conséquence directe de la 1)a)

Par encadrement (Théorème des deux gendarmes)
$\fbox{\displaystyle\lim_{x\to 0^+}f(x)=2}$

1)c) Même démarche que pour la 1)a) pour étudier le cas x < 0

$E\left(\frac{2}{x}\right)\le \frac{2}{x}<E\left(\frac{2}{x}\right)+1$

Ici, x<0, donc en multipliant par x, le sens des inégalités change.

Après transformation, on obtient ainsi dans ce cas

$2-x<f(x)\le 2$

Le théorème des deux gendarmes permet donc de déduire:
$\fbox{\displaystyle\lim_{x\to 0^-}f(x)=2}$

En 0, la limite à droite et la limite à gauche sont égales (à 2), ce qui permet de conclure :
$\fbox{\displaystyle\lim_{x\to 0}f(x)=2}$

2. Pour x > 0

$0<\frac{2}{x}<1$ donc $E\left(\frac{2}{x}\right)=0$

On peut déduire que f(x)=0 pour tout x > 2, donc en particulier lorsque x tend vers $+\infty$, d'où
$\fbox{\displaystyle\lim_{x\to +\infty }f(x)=0}$

3. Etude lorsque x tend vers $-\infty$

Lorsque x tend vers $-\infty$, $\frac{2}{x}$ tend vers $0^{-}$ donc $E\left(\frac{2}{x}\right)$ tend vers $-1$

Avec la règle des signes du quotient, on peut déduire:

$\fbox{\displaystyle\lim_{x\to -\infty }f(x)=+\infty}$

Un schéma pour illustration graphique

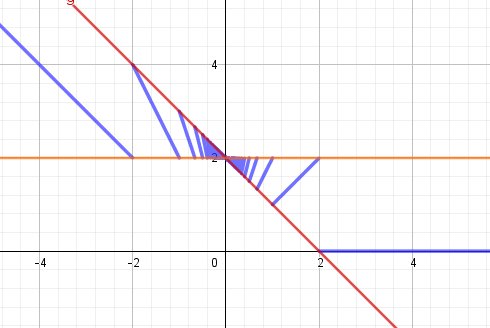
Les droites d'équations y=2 et y=2-x sont en rouge
La représentation graphique de f est en bleu
(Pour être plus précis, il faut compléter le schéma en indiquant lorsque les extrèmités des segments ou demi-droites sont prises ou pas)