Fonction acec valeurs absolues - Limites

[hafud]

Bonjour pouvez-vous m'aidez
Considérons la fonction $f$ défini par
$f(x)=(2x+|x|+|x-1|)/(x-2)$

1. montrer que $limf(x)=4$ en +∞
   et calculer $limf(x)$ en -∞
2. déterminer $limf(x)$ en 2 si x>2 et $limf(x)$ en $2$ si x<2

[Noemi]

Bonsoir hafud,

Tu n'as pas résolu les autres exercices et tu continues à en proposer d'autres.

Indique tes éléments de réponse et la question qui te pose problème.

Ecris la fonction dans le cas ou $x$ tend vers +00 puis vers -00.

[mtschoon]

Bonjour hafud

Comme dit Noemi, tu n'as pas résolu les autres exercices et tu continues à en proposer d'autres.

Méthode générale pour traiter tout exercice avec de valeurs absolues : les supprimer

Rappel :
Pour $a>0:|a|=a$
Pour $a=0:|a|=0$
Pour $a<0:|a|=-a$

On peut écrire plus simplement :
Pour $a\ge 0:|a|=a$
Pour $a\le 0:|a|=-a$

f(x) peut donc s'exprimer de 3 façons suivant x :

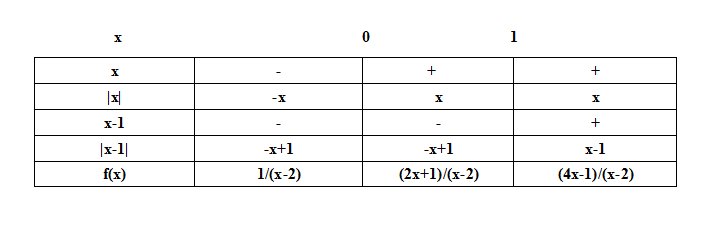
Bonne réflexion !

[hafud]

@mtschoon on choisit $4x-1/x-2$

[Noemi]

@hafud

Oui dans le cas ou $x$ tend vers +00.

[hafud]

@Noemi oui l'autre (2x-x-x+1)/(x-2)=0

[Noemi]

@hafud

Oui simplifie l'expression et calcule la limite.

[hafud]

@Noemi il me donne 0

[Noemi]

@hafud

Oui, on pourrait préciser 0-

[hafud]

@Noemi pour la limite en 2^+ c'est +∞ et 2^- c'est -∞

[Noemi]

@hafud

C'est correct.

[hafud]

@Noemi merci