Axe de symétrie et intervalle de fonction 1erS

Bonsoir,
Voilà mon problème, je travaille sur un exercice depuis un petit moment et je bloque à deux question : la 5 et la 6.
Afin de faciliter la compréhension de l’exercice je vais récrire les question avec le résultat obtenus .

On considère la fonction f définie par f(x)=1- $2x2−2x+3\frac{2}{x^2-2x+3}$

1-Montrer que f est défini pour tout réel x
Réponse:f(x) est définie pour tout réel x
Ps: je “transforme” la forme de la fonction pour faciliter les calculs à suivre:
$x2−2x+1x2−2x+3\frac{x^2-2x+1}{x^2-2x+3}$
2-Résoudre l’équation f(x)=0
Réponse: f(x)= 0 <=> x = 1

3-Soit (C) la courbe représentative de f. Tracer sur votre copie (C)
Réponse:La courbe est faite à main levée mais on peut observer que la courbe ne dépasse jamais y=1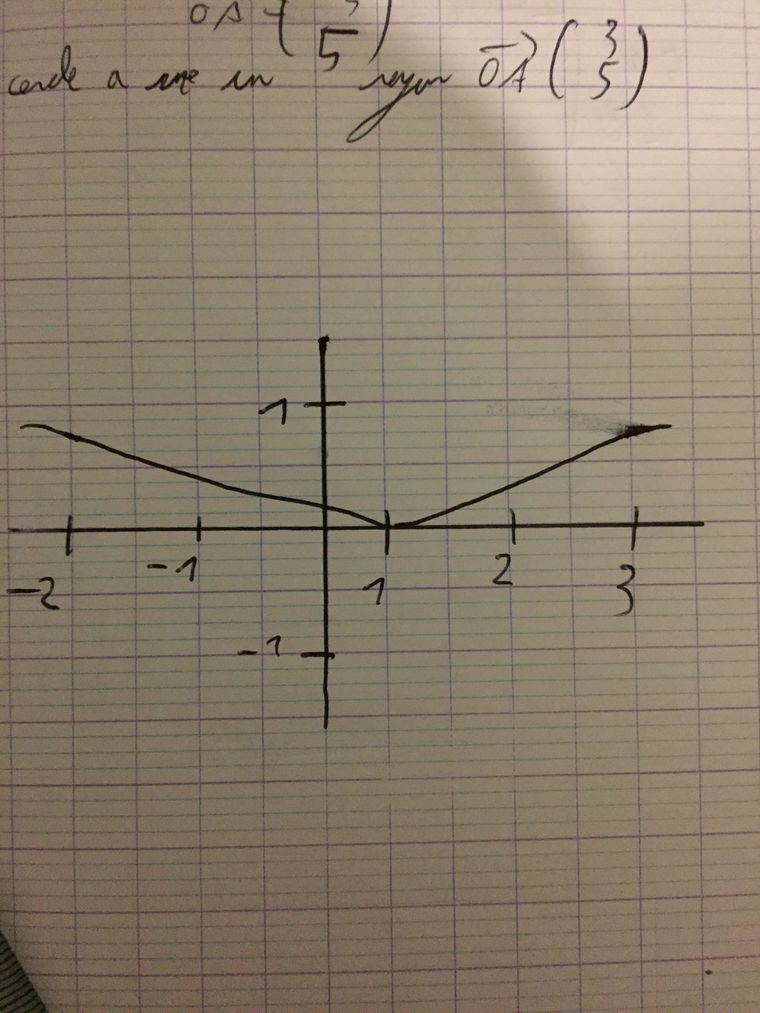

4-En déduire le tableau de variation de (C)
Réponse :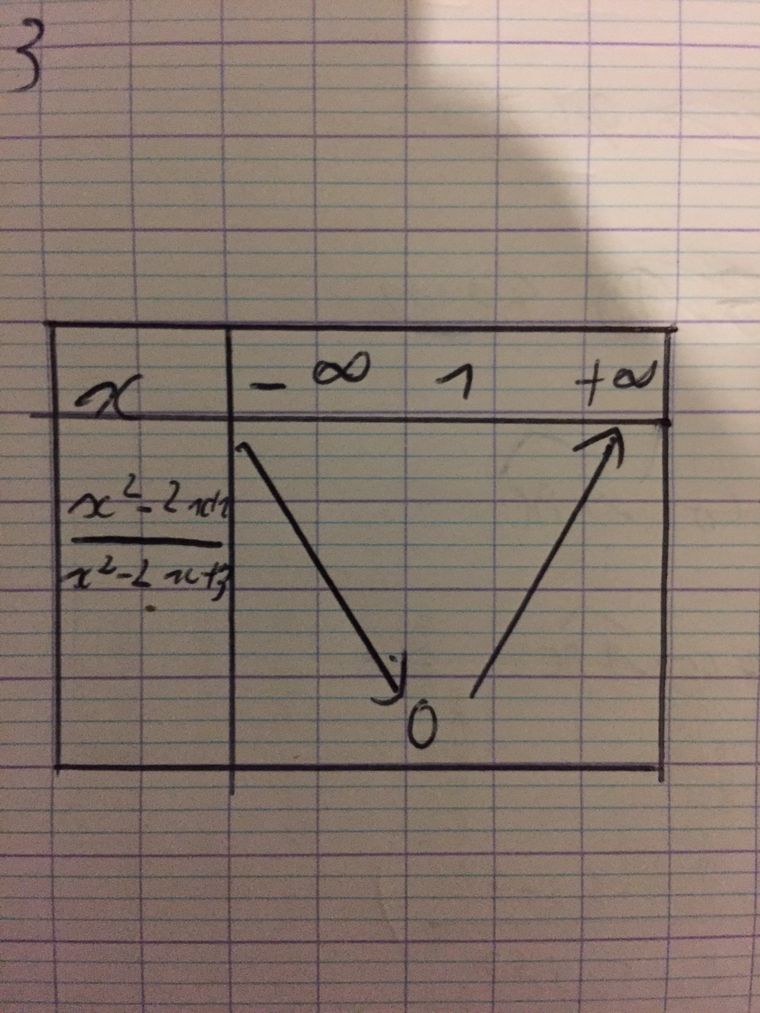

C’est maintenant que sa se complique pour moi.
5-Déterminer un axe de symétrie de (C)
Je pense l’axe de symétrie et 1 mais je ne sait pas comment l’expliquer.
6-Montrer que pour tout x réel
$\leq f(x) \leq 1$
Pour cette question j’en n’ai pas de réponse

Merci d’avoir pris le temps de lire.

Bonsoir omgabot,

5)Fais un changement de variable en posant X = x-1 et montre que la fonction f(X) est paire.

Montre que $\leq 0$ et $\geq 0$ .

Bonsoir @Noemi ,
Merci je vais faire sa.

@omgabot

Tu peux indiquer ta réponse si tu souhaites une correction.

@Noemi
J’ai juste une question.
Comment f(X) est paire puisque une fonction paire est une fonction symétrique par apport à l’axe des ordonnées?

@omgabot

En posant X = x-1, si x = 1 ; X = 0 donc le nouvel axe des ordonnées correspond à x = 1.

@Noemi
J’ai remplacé par X=(x-1) mais j’obtiens
$x2−2x+4x2−2x+6\frac{x^2-2x+4}{x^2-2x+6}$
J’ai essayé de faire le discriminant pour $x^2$ -2x+4 et $x^2$ -2x+6 mais j’obtiens respectivement-12 et -20

@omgabot

Vérifie tes calculs, tu dois remplacer $x$ par $X + 1$ et trouver : $X2X2+2\dfrac{X^2}{X^2+2}$ .

@Noemi
J’ai remplacé par x+1 mais je trouve:
$x2x2+2\frac{x^2}{x^2+2}$

@omgabot

C'est juste.

@Noemi
Donc je peux dire que la fonction est paire ?

@omgabot

Il faut démontrer que la fonction est paire.

@Noemi
Pour sa je remplace f(x) par f(-x) comme sa:
$−x2−x2+2\frac{-x^2}{-x^2+2}$
Se qui fait:
$x2x2+2\frac{x^2}{x^2+2}$
Donc f(x) = f(-x)
Donc la fonction est paire
?

@omgabot

Oui f(-X) = f(X) et il faut préciser que si $X$ appartient à $D_f$ , $- X$ appartient aussi à $D_f$ .
Donc la fonction est paire.

@Noemi
D’accord merci je vais essayer de faire la question 6.Si je bloque encore je demanderai de l’aide

@omgabot

Propose tes réponses si tu souhaites une correction.

@Noemi
J’ai trouvé pour f(x) $\leq 0$ :
$2x2−4x+4x2−2x+3\frac{2x^2-4x+4}{x^2-2x+3}$
Et pour f(x)+ $\geq 0$ :
- $2x2−2x+3\frac{2}{x^2-2x+3}$

@omgabot

Tu as inversé les deux écritures, Démontre que la deuxième est toujours négative et la première toujours positive.

@Noemi
Oui j’ai tapé trop vite mais sur ma feuille c’est correct.
Comment je doit procéder pour montrer que c’est constant?
Je pensais utiliser les discriminants et montrer qu’il n’y a pas de solution

@omgabot

Oui montre que chaque polynôme du second degré est du signe du terme de plus haut degré en montrant que son discriminant est négatif.

@Noemi
D’accord je pense pouvoir me débrouiller maintenant. Je posterai un autre message si besoin.
Merci pour toute l’aide et bonsoir

@omgabot

Bonsoir et n'hésite pas à poster si besoin.