Convergence d'une suite (somme de Riemann)

Bonsoir tout le monde!
J'ai trouvé un problème pour résoudre cette question
Prouver que la suite (Un) est convergente en indiquant sa limite ;
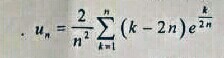
IMG-20190307-WA0003-1-1~2.jpg
J'ai essayé de résoudre ce problème avec la somme de Riemann et j'ai trouvé cette intégral
(Intégrale de 0 à 1 de ${e^{x/2}(2x-4)}$ )après calculer j'ai trouvé $12e^{1/2}$ mais je ne suis pas sûre de cette réponse, merci de me corriger!

@sui bonjour,
La somme de Riemann me semble tout à fait adaptée

$b−an∑k=1k=nf(a+kb−an)\displaystyle \dfrac{b-a}{n}\sum_{k=1}^{k=n}f(a+k\dfrac{b-a}{n})$ converge vers $∫abf(x)dx\displaystyle \int_{a}^{b}f(x) dx$ lorque n tend vers $+∞+\infty$ , avec la condition d'intégrabilité de f réalisée sur [a,b]

Pour transformer $U_n$ je commencerais par diviser $(k - 2 n)$ par $n$ en mettant ainsi $n$ en facteur

$Un=2n∑k=1n\displaystyle U_n=\dfrac{2}{n}\sum_{k=1}^n$ $(kn−2)ek/n(\dfrac{k}{n}-2)\sqrt{e^{k/n}}$
$Un=2[1n∑k=1n(kn−2)ek/n]\displaystyle U_n=2\biggl[\dfrac{1}{n}\sum_{k=1}^n(\dfrac{k}{n}-2)\sqrt{e^{k/n}}\biggl]$

Sauf erreur, tu peux prendre $f(x)=(x−2)exf(x)=(x-2)\sqrt{e^x}$ , $a = 0$ , $b - a = 1$ d'où $b = 1$

Vérifie mes transformations et continue.

Merci @mtschoon ! c'est la même chose que j'ai fais, sauf que j'ai pris a=0 et b=1
Je n'ai pas compris pourquoi vous avez choisi ces valeurs pour a et b ?

Tu as tout à fait raison a=0 et b=1, vu que la quantité entre crochets vaut

$1n∑k=1nf(kn)\displaystyle \dfrac{1}{n}\sum_{k=1}^nf(\dfrac{k}{n})$

La limite de la suite est donc $2∫01(x−2)exdx2\int_0^1(x-2)\sqrt{e^x}dx$ ou comme tu l'as écrit $∫01(2x−4)exdx\int_0^1(2x-4)\sqrt {e^x}dx$

Sauf erreur,une primitive doit valoir $(4x−16)ex(4x-16)\sqrt{e^x}$

Entre les bornes 0 et 1, tu dois obtenir $−12e+16-12\sqrt{e}+16$

Peut-être que tu as fait tout simplement une erreur dans les calculs aux bornes.

Vérifie.

@mtschoon oui l'intégral est correcte j'ai fait une petite bêtise au calcul!
Merciiii

C'est très bien d'avoir rectifié ta petite erreur. Bon travail !