DM zone de baignade- inéquation du second degré
-
PPolaris dernière édition par mtschoon
Bonjour,
j'ai un dm de maths à rendre pour demain mais je ne sais absolument pas comment faire.
Voici le sujet :Marie Pierre doit délimiter la zone de baignade qu'elle va surveiller. Elle dispose pour cela d'une ligne qui a une longueur de 60 mètres.
Pour des questions de sécurité, la zone de baignade doit être rectangulaire et avoir une superficie supérieure à 400m².
On note L la longueur et l la largeur, en m, de la zone de baignade.1)Traduire les données de l'exercice par une équation et une inéquation d'inconnu L et l.
- montrer que résoudre le problème revient à résoudre le système
{-2l²+60l-400⩾0
{L=60-2l
3)voici différentes écritures de l'expression -2l²+60l-400 obtenue avec un logiciel de calcul formel.
a)utiliser la forme la plus adaptée pour résoudre l'inéquation -2l²+60l-400⩾0.
b)En déduire les dimensions possibles pour la zone de baignade que Marie Pierre doit surveiller.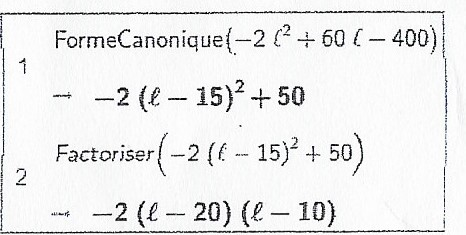
- montrer que résoudre le problème revient à résoudre le système
-
PPolaris dernière édition par
je pense que pour le 1) sa doit etre L60*l60⩽400 mais je suis pas sur.
-
mtschoon dernière édition par mtschoon

@enzo , bonjour,
Je te donne un schéma pour essayer de t'éclairer et des pistes pour démarrer ton exercice.
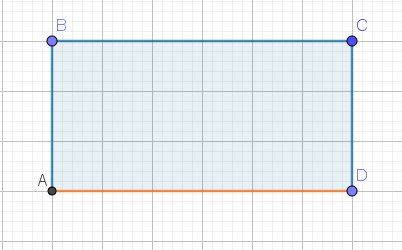
Suppose que :
la rive est [AD] (en rouge)
la zone de baignade est l'intérieur du rectangle ABCD (en bleu clair)
la ligne est [AB]+[BC]+[CD] (en bleu foncé)AB=CD=l et BC=L
La condition relative à la ligne est : AB+BC+CD=60AB+BC+CD=60AB+BC+CD=60,
c'est à dire l+L+l=60l+L+l=60l+L+l=60
c'est à dire 2l+L=602l+L=602l+L=60
c'est à dire L=60-2l\fbox{L=60-2l}L=60-2lLa condition relative à la superficie est :
AB×BC≥400AB \times BC\ge 400AB×BC≥400
c'est à dire l×L≥400l\times L \ge 400l×L≥400
c'est à dire $\fbox{l\times (60-2l) \ge 400}$Essaie de poursuivre.
-
PPolaris dernière édition par
C'est bon. J'ai factorisé et passé le 400 en -400. sa donne l'inéquation de la question 2).
Pour le 3), j'ai essayé de développé les 3 formes mais j'ai pas réussi. C'est peut-être à cause de mon très bas niveau en maths mais je pense plutôt qu'il faut faire un tableau de variation ou quelque chose comme ça. Mais je ne sais pas pour quelle forme le faire ni comment le faire si c'est sa.
-
Bonjour enzo,
Pour la question 3, il faut déterminer les valeurs de xxx pour lesquelles le polynôme est positif, donc faire un tableau de signes est une méthode.
Donc utilise la formule "factoriser ".
-
PPolaris dernière édition par

J'ai fait sa et je suis à peu près sur que c'est juste mais je ne comprend pas comment je peux en déduire les dimensions possibles pour la zone de baignade.
-
mtschoon dernière édition par mtschoon

@enzo,
Ton tableau de signes est bon, mais n'oublie pas que l'inéquation est
−2(l−20)(l−10)≥0-2(l-20)(l-10) \ge 0−2(l−20)(l−10)≥0−2(l−20)(l−10)-2(l-20)(l-10)−2(l−20)(l−10) est donc positif pour $\fbox{10\le l \le 20}$
Tu en déduis ensuite l'encadrement correspondant de L
-
PPolaris dernière édition par
Ok. Merci beaucoup. J'ai juste une dernière question : comment on peut montrer clairement que résoudre le problème revient à résoudre le système ?
-
mtschoon dernière édition par

J'espère que tu as trouvé l'encadrement de L
(Tu peux le donner si tu as besoin d'une vérification)Résoudre le problème revient à résoudre le système vu que le système est composé de l'équation et de l'inéquation représentant les deux conditions de l'énoncé (relatives à la ligne et à la superficie).
-
PPolaris dernière édition par
L'encadrement est [10;20].
Merci de votre aide .
-
mtschoon dernière édition par mtschoon

Attention.
On te demande les dimensions possibles pour la zone de baignade .
Il faut donc que tu donnes les dimensions possibles de l (largeur) et L (longueur).Pour la largeur l , c'est bon : 10≤l≤2010 \le l \le 2010≤l≤20 c'est à dire $\fbox{l\in[10,20]}$
Comme déjà indiqué, il faut en déduire les dimensions possibles de la longueur L
Utilise l'égalité L=−2l+60L=-2l+60L=−2l+60 et l'encadrement de l
10≤l≤2010 \le l \le 2010≤l≤20
En multipliant par -2, on change le sens de l'inégalité :
−40≤−2l≤−20-40 \le -2l \le -20−40≤−2l≤−20
En ajoutant 60 à chaque membre, tu obtiendras l'encadrement de −2l+60-2l+60−2l+60 c'est à dire de LIndique ta réponse si tu le souhaites.