Exercice sur les suites

Bonsoir, j'ai une question d'un exercice que je n'y arrive pas vraiment...
On admet que la suite de terme général $2/3)^n$ a pour limite zéro.
Démontrer en utilisant le théorème admis, et la définition d'une suite qui a pour limite 1, que la suite U(n) a pour limite 1.

Dans l'exercice on ne connait seulement $Un+1=f(Un)=2Un+1U_{n+1}= f(U_n) = \dfrac{2}{U_n+1}$

Merci

(Formule écrite en Latex par la modération)

Bonsoir Constance,

Vérifie l'énoncé, notamment la définition de la suite $U_{n+1}$ .

@Noemi U(n+1)= f (Un) et on a f(x)=2/(x+1)

@Constance ,
comme te l'a dit @Noemi , vérifie ton énoncé !
On peut même dire : donne l'énoncé !

Tu te contentes d'indiquer la conclusion à prouver sans donner les questions précédentes ...

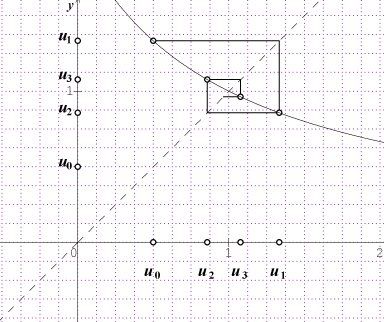
Pour illustrer le comportement de la suite, je joins un schéma classique.
La portion utile de la représentation graphique de la fonction f est en trait continu
La représentation graphique de la droite d'équation y=x est en traits discontinus.
A partir de $U_0=1/2$ mis sur l'axes des abscisses, on peut construire les termes successifs de la suite (voir cours)

Sur le schéma, $U_0 ...U_3$ sont représentés sur les 2 axes de coordonnées. Tu peux compléter.

On peut ainsi conjecturer que $U_n)$ converge vers 1.

Pour avoir des bribes de démonstration, voir l'autre discussion que tu as ouverte :
https://forum.mathforu.com/topic/30687/exercice-valeur-absolue/6

Une autre fois, si tu as besoin, ouvre une seule discussion, écrit l'énoncé entier, indique les questions que tu as résolues et celles où tu bloques.
Nous pourrons ainsi t'aider utilement.