Une fonction dans un trapèze

Bonsoir!
Alors voilà j’ai un Dm à rendre pour lundi et j’ai un exercice qui me pose problème... (ex 4 et les deux derniers de l’exercice 3)
Je n’arrive pas à commencer et pourtant ça fait une semaine que j’essaie!
Est ce qu’une âme charitable pourrait m’aider s’il vous plait... Mon devoir est a rendre pour la semaine prochaine
Merci d’avance !

Voici l’énoncé:

La figure si contre représente un trapèze ABCD tel que AB = 6cm ; BC = 2cm ; AD = 8cm
Le point M décrit [AB] et on construit les points N et P des segments [CD] et [AD] tels que AMNP est un rectangle.
On note x = AM, exprimé en cm, et f(x) l’aire de AMNP exprimé en cm carré
![Figure Trapèze]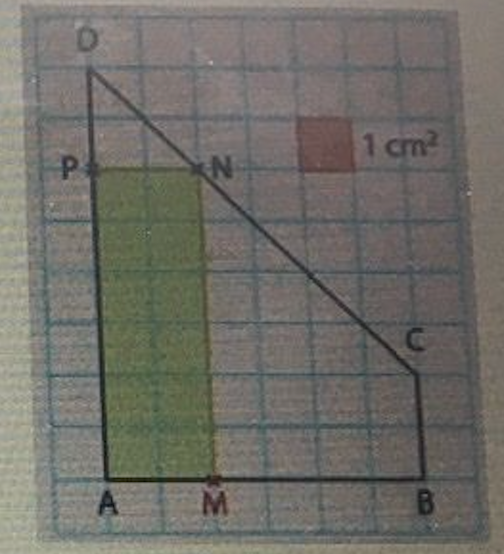 2773b098-11be-41e8-9f36-9a79e376aba9-Figure Trapèze.png

1.a. Lire ,la valeur de x sur la figure ci-contre et calculer f(x) pour cette valeur de x.

b. Quand M décrit le segment [AB], quelles valeurs prends AM? Ecrire leurs ensembles de Df.

2.a. Justifier que le triangle DPN est rectangle isocèle en P.
b. En déduire, en fonction de x, PN puis AP, puis f(x)
c. Demontrer que pour tout de Df,
f(x) = 16 - (x-4) au carré

3.a Tableau
x 0 0,5 1 1,5 2 3 4 5 7
f(x)

Bonsoir baptsypf,

Le scan de l'énoncé est interdit sur ce forum. Seuls les schémas ou figures sont autorisés.
Recopie l'énoncé et indique tes éléments de réponse si tu veux obtenir de l'aide.

Pour le 1) indique les valeurs de AM et de AP puis de l'aire.

@Noemi
D’accord je vais faire ça merci

Bonjour baptsypf,

Maintenant que tu as recopié l'énoncé, indique tes éléments de réponse.

a) Sur le schéma,
AM = x = 2 cm
De même AP = 6 cm
Puis l'aire f(x) soit AM x AP = .....

b) Combien de valeurs entières possibles du point A au point B ? de 0 à .....

@Noemi
Merci noemi j’étais vraiment bloqué sur la question 1.b car je n’avais pas bien saisi la question
C’est vraiment très gentil d’avoir répondu
Pourrais tu juste me guider pour la question 2.b et 2.c s’il te plait
Ça serai vraiment super
Merci d’avance!

@baptsypf

$A M = x$ , comme $P N = A M$ alors $P N = . . . .$

$A P = A D - D P$ et $D P = P N$
donc $A P = . . . .$

Puis tu calcules l'aire ...
Soit $f (x) = . . . . .$

Je te laisse compléter les .....

@Noemi
D’accord merci
PN=AM= x

AP=DA-DP
AP= 8-x

Donc f(x)= x X (8-x)
= -x au carré + 8x

J’ai compris merci!
Mais pour le 2.c, comment je fais?

@Noemi et @baptsypf , bonjour,
@baptsypf , en attendant que Noemi soit là, je regarde ta dernière question
Oui, f(x)=−x²+8x
Tu peux te contenter de faire la vérification
Pars de (x−4)²−16
Développe l'identité remarquable (x-4)² et remplace dans 16-(x-4)² , simplifie et tu dois trouver -x²+8x

La vérification est la méthode la plus simple .

Si tu veux faire encore mieux.

Tu pars de ta réponse -x²+8x et tu la transformes

−x²+8x=−x²+8x−16+16=−(x²−8x+16)+16

Tu dois reconnaître l'identité remarquable (x-4)² et trouver le résultat souhaité.

@mtschoon
Merci beaucoup c’est très gentil de votre part de m’avoir aider.
Bon dimanche !

Bonjour baptsypf,

J'espère que tu as tout compris.
As tu terminé l'exercice ?