dm sur un probleme de triangles

[Lilia Sahridj]

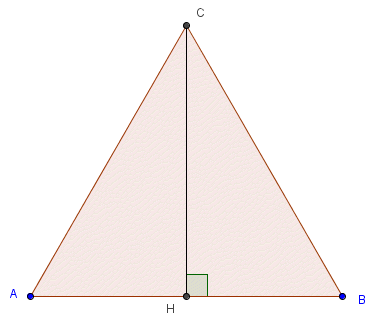
bonjour pouvez vous m’aidez a résoudre a ce problème merci

abc est un triangle équilatéral CH =2

1. calculer la longueur des cotes du triangle
2. en déduire la valeur exacte de sin 60°

[Noemi]

Bonsoir Lilia-Sahridj,

1. Pour calculer la longueur d'un côté du triangle :
   applique la propriété de Pythagore dans le triangle ACH.

[mtschoon]

@Noemi et @Lilia-Sahridj , bonjour,

@Lilia-Sahridj , un petit coup de pouce de plus, si besoin

Si ton cours te donne la formule de la hauteur d'un triangle équilatéral de côté a, tu peux l'appliquer directement
$CH=\frac{a\sqrt{3}}{2}$ <=> $2=\frac{a\sqrt{3}}{2}$
Tu peux ainsi trouver a directement.

Sinon, comme te dit Noemi, utilise le théorème de Pythagore
$A{C}^2=A{H}^2+H{C}^2$
En appelant a la longueur des côtés du triangle ABC
$a^2=(\frac{a}{2}{)}^2+2^2$ <=> $a^2=\frac{a^2}{4}+4$

Tu trouveras a (positif, bien sûr)

Tiens nous au courant de ton avancée.