3. Trouver l'équation d'un cercle à partir de 3 points

Trouver l'équation d'un cercle à partir de 3 points

  • Leass

    Bonsoir , me voila bloqué lors de mon exercice , je ne comprends pas comment toruver l'équation d'un cercle a partir des points A(-3;3) B(1;3) C(3;-3)

    N 1 réponse
  • N
    Modérateurs

    Bonsoir Leass,

    Equation d'un cercle : (x−a)2+(y−b)2=R2(x-a)^2 + (y-b)^2 = R^2(x−a)2+(y−b)2=R2
    Tu as trois inconnues, tu dois écrire trois équations.
    Utilise les coordonnées des points pour écrire les équations puis résous le système.
    Pour le point A cela donne : (-3-a)^2 + (3-b)^2 = R^2

    Indique tes éléments de réponse si tu souhaites une correction.

    Leass 1 réponse
  • Leass

    @Noemi merci , cela est-il bon pour B(1-a)^2+(3-b)^2=r^2 et pour C(3-a)^2+(-3-b)^2=r^2 ? merci

    N 1 réponse
  • Leass

    Et lorsque j'ai cela que doit-je faire ?

  • N
    Modérateurs

    @Leass

    C'est correct : tu obtiens le système :
    (−3−a)2+(3−b)2=r2(-3-a)^2+(3-b)^2 = r^2 (−3−a)2+(3−b)2=r2 (1)
    (1−a)2+(3−b)2=r2(1-a)^2 + (3-b)^2 = r^2 (1−a)2+(3−b)2=r2(2)
    (3−a)2+(−3−b)2=r2(3-a)^2 + (-3-b)^2 = r^2(3−a)2+(−3−b)2=r2 (3)

    Pour trouver aaa calcule (1) - (2).

  • Leass

    ok donc j'ai a = 7+6a+2a^2-6b+b^2 et que doit-je faire maintenant ?

    N 1 réponse
  • N
    Modérateurs

    @Leass

    Si tu calcules (1) - (2) cela donne :
    (−3−a)2−(1−a)2=0(-3-a)^2 -(1-a)^2 = 0(−3−a)2−(1−a)2=0
    si tu développes
    9+6a+a2−1+2a−a2=09 + 6a + a^2 - 1 + 2a - a^2 = 09+6a+a2−1+2a−a2=0
    tu résous l'équation pour trouver la valeur de aaa

    Pour trouver bbb tu fais (3) - (2) en remplaçant aaa par sa valeur.

  • Leass

    je ne comprends pas quand tu dis remplace a par sa valeur car si je fais (3)-(2) ca me donne (-3-b)^2-(3-b)^2 donc quand est-ce que je dois remplacer a ?

    N 1 réponse
  • N
    Modérateurs

    @Leass

    (3) - (2) donne : (3−a)2+(−3−b)2−(1−a)2−(3−b)2=r2−r2=0(3-a)^2 + (-3-b)^2 - (1-a)^2 - (3-b)^2 = r^2 - r^2 = 0(3−a)2+(−3−b)2−(1−a)2−(3−b)2=r2−r2=0

  • Leass

    ah ok merci

  • Leass

    si je calcule bien j'ai -12-2b^2=0 j'ai bon ?

  • Leass

    mais lorsuqe je resous l'equation pour trouver b je triuve (-b^2)^1/2 et je ne pense pas que c'est nrmal

    N 1 réponse
  • N
    Modérateurs

    @Leass

    Tu as fait des erreurs dans le calcul
    as-tu trouvé -1 pour aaa ?
    l'équation (3) - (2) devient :
    16+(−3−b)2−4−(3−b)2=016 + (-3-b)^2 -4 -(3-b)^2 = 016+(−3−b)2−4−(3−b)2=0
    16+9+6b+b2−4−9+6b−b2=016 + 9 + 6b + b^2 - 4 - 9 + 6b - b^2 = 016+9+6b+b2−4−9+6b−b2=0
    soit 12+12b=012 + 12b = 012+12b=0
    donc b=....b = ....b=....

  • mtschoon

    Bonjour,

    Pour consultation éventuelle,
    Une autre méthode possible : géométrie analytique
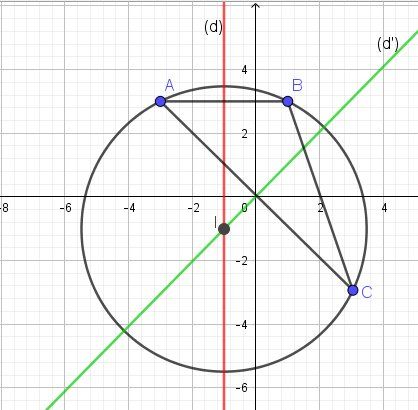
    cercle.jpg
    Pistes,
    Soit I le centre du cercle et R son rayon.
    IA=IB=IC donc I est le point d'intersection des médiatrices du triangle ABC
    Soit (d) la médiatrice de [AB]
    (AB) est parallèle à l'axe des abscisses donc (d) est parallèle à l'axe des ordonnées.Elle passe par le milieu de [AB] qui a pour abscisse −3+12=−1\dfrac{-3+1}{2}=-12−3+1​=−1.
    Tout point de (d) vérifie x=-1 donc $\fbox{x_I=-1}$
    Soit (d') la médiatrice de [AC]
    O est le milieu de [AC].
    L'équation de (AC) est y=-x ("seconde bissectrice des axes")
    L'équation de (d') ("première bissectrice des axes") a pour équation y=x donc yI=xIy_I=x_IyI​=xI​ donc $\fbox{y_I=-1}$

    R=OA=(−3−0)2+(3−0)2R=OA=\sqrt{(-3-0)^2+(3-0)^2}R=OA=(−3−0)2+(3−0)2​ donc $\fbox{R= \sqrt{20}}$

    L'équation du cercle est donc : (x−xI)2+(y−yI)2=R2(x-x_I)^2+(y-y_I)^2=R^2(x−xI​)2+(y−yI​)2=R2
    c'est à dire :
    $\fbox{(x+1)^2+(y+1)^2=20}$

Se connecter pour répondre