Aide Limites et asymptotes

[Oce942]

Bonjour,
J'aurai besoin d'aide pour un exercice de maths s'il vous plaît...

Soir f la fonction définie sur ]-infini;1[ U ]1;+infini[ par f(x)=(2x^3+2x^2-10x+11)/2(x-1)^2

Calculer la limite de f aux bornes de son intervalle de définition.
Déterminer les asymptotes à la courbe.
Étudier la position relative de la courbe C et de la droite d'équation y=x+3
Merci d'avance pour votre aide

[Noemi]

Bonjour Oce942,

Indique tes éléments de réponse et la question qui te pose problème.
Pour les limites en $\infty$, tu choisis le terme de plus haut degré du numérateur et du dénominateur et tu calcules la limite.
Soit $lim\frac{2x^3}{2x^2}$

Pour les limites et 1+ et 1- analyse la limite du numérateur et du dénominateur puis de $f(x)$.

Pour les asymptotes tu déduis l'asymptote verticale du résultat d'une limite calculée précédemment.
Pour l'asymptote oblique, commence par calculer le limite de $\frac{f(x)}{x}$.

Pour étudier la position relative de la courbe C par rapport à la droite d'équation $y=x+3$, étudie le signe de $f(x)-y$.

Indique tes éléments de réponse si tu souhaites une correction.

[mtschoon]

@Noemi et @Oce942 , bonjour,

@Oce942
Comme te l'a indiqué Noemi, reposte si tu as besoin d'aide .

Je regarde tes questions.
Pour l'asymptote oblique, cela m'étonne qu'aucune indication ne soit donnée dans l'énoncé.
J'aurais pensé que la droite d'équation y=x+3 t'aurait été indiquée et qu'on t'aurait demandé de prouver qu'elle était asymptote oblique.
Ainsi, tu n'aurais seulement à prouver que $\underset{\pm \infty }{\lim }[f(x)-(x+3)]=0$

Une idée aurait été intéressante :
que l'énoncé te demande en début de questions, de prouver que :
$\fbox{f(x)=x+3+\dfrac{5}{2(x-1)^2}}$.
ça t'aurait aidé(e) pour les limites, l'asymptote oblique et la position relative de la courbe C et de l'asymptote oblique.
Ce serait totalement dans l'esprit du cours de Terminale.

Es-tu bien sûr(e) qu'il n'y ait pas eu cette question dans ton énoncé ? ? ?

Cela me surprend que tu aies vu la méthode générale pour trouver l'asymptote oblique....
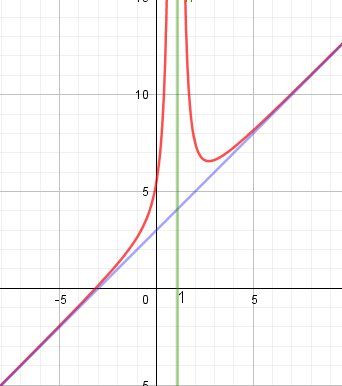
Evidemment, si c'est le cas, il faut que tu prouves que $\underset{\pm \infty }{\lim }\frac{f(x)}{x}=1$ et que $\underset{\pm \infty }{\lim }[f(x)-x]=3$

A toute fin utile , je te donne le schéma (courbe, asymptote verticale (x=1) et asymptote oblique (y=x+3)).
Tu peux bien sûr obtenir le graphique sur ta calculette et ainsi pouvoir vérifier tes réponses.