Exercice sur le théorème des valeurs intermédiaires
-
?Un Ancien Utilisateur dernière édition par
Bonjour à tous comment allez vous ?
J'aimerais savoir si vous pouviez m'aider parce que j'avoue que je ne suis vraiment pas douée en maths et on vient de commencer ce chapitre.
Alors voici l'exercice:
Soit f(x)=-3x^3+4x+1 Montrer que l'équation f(x)=0,5 et qu'elle admet exactement 3 solutions.
Merci d'avance pour vos réponses
-
mtschoon dernière édition par mtschoon

@Loan-Bremont , bonjour,
Piste,
−3x3+4x+1=0.5-3x^3+4x+1 =0.5−3x3+4x+1=0.5 <=>−3x3+4x+1−0.5=0-3x^3+4x+1 -0.5=0−3x3+4x+1−0.5=0 <=>$\fbox{-3x^3+4x+0.5 =0}$
Tu peux poser $\fbox{g(x)=-3x^3+4x+0.5}$
Tu étudies les variations de g su R puis tu utilises le TDI sur chacun des trois intervalles où g est strictement décroissante ou strictement croissante.
Pour les variations de g, tu dois trouver après calculs :
g strictement décroissante pour x≤23x \le\dfrac{2}{3}x≤32
g a un minimum (relatif) égal à -2318\dfrac{23}{18}1823 pour x=−23-\dfrac{2}{3}−32
g strictement croissante pour −23≤x≤+23-\dfrac{2}{3} \le x\le +\dfrac{2}{3}−32≤x≤+32
g a un maximum (relatif) égal à 4118\dfrac{41}{18}1841 pour x=23\dfrac{2}{3}32
g strictement décroissante pour x≥23x \ge \dfrac{2}{3}x≥32
Reposte si tu n'y arrives pas.
-
?Un Ancien Utilisateur dernière édition par
@mtschoon Bonjour,
Ok merci je galère pour les tableaux de signes et de variations je comprends vraiment rien je dois d'abord calculer la limite de f(x) non ?
-
mtschoon dernière édition par mtschoon

@Loan-Bremont ,
Commence par calculer la dérivée g'(x) et étudie son signe ;
Tu auras ainsi le sens de variation de la fonction g (que je t'ai donné pour que tu puisses vérifier) .et tu mettras tout ça sous forme de tableau de variation.Tu dois trouver g′(x)=−9x2+4g'(x)=-9x^2+4g′(x)=−9x2+4
puis
Tu dois trouver un tableau de variation ressemblant à ça :
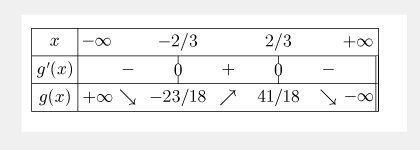
(le tableau n'est pas très bien fait car en Latex, ce n'est pas très commode...)
-
?Un Ancien Utilisateur dernière édition par
@mtschoon J'ai bien cette dérivée par contre pour le calcul des limites je me souviens plus
-
?Un Ancien Utilisateur dernière édition par
@mtschoon On fait delta non ?
-
mtschoon dernière édition par mtschoon

Si tu parles de la recherche des valeurs qui annulent la dérivée, vu que c'est un cas simple, tu n'as pas besoin de Δ\DeltaΔ
−9x2+4=0-9x^2+4=0−9x2+4=0 <=> −9x2=−4-9x^2=-4−9x2=−4 <=> x2=−4−9x^2=\dfrac{-4}{-9}x2=−9−4 <=> x2=49x^2=\dfrac{4}{9}x2=94
les nombres dont la carré vaut 49\dfrac{4}{9}94 sont x=... et x=... (je te laisse trouver)
Lorsque tu as les deux solutions de g'(x)=0, vu que g'(x) est un polynôme du second degré avec a=-3, tu appliques le théorème usuel (signe de a, signe de -a, signe de a)
-
mtschoon dernière édition par

Les limites semblent aussi de te poser problème.
Vu que tu postes en Terminale S, je pense que tu sais que, en +∞+\infty+∞ ou −∞-\infty−∞, la limite d'un polynôme est la limite de son terme de plus fort degré (ce théorème t'évite une mise en facteur)Tu cherches donc le limite de −3x3-3x^3−3x3
Lorsque x tend vers +∞+\infty+∞, x3x^3x3 tend vers +∞+\infty+∞, −3x3-3x^3−3x3 tend vers −∞-\infty−∞ donc g(x)g(x)g(x) tend vers −∞-\infty−∞
Applique la même démarche lorsque x tend vers −∞-\infty−∞
-
mtschoon dernière édition par mtschoon

Conclusions pour consultation éventuelle
1er cas : x∈]−∞,−23]x\in \biggl]-\infty,-\dfrac{2}{3}\biggl]x∈]−∞,−32]
g est définie, dérivable donc continue et strictement décroissante donc bijective de de ]−∞,−23]\biggl]-\infty,-\dfrac{2}{3}\biggl]]−∞,−32] vers [−2318,+∞[\biggl[\dfrac{-23}{18}, +\infty\biggl[[18−23,+∞[
0∈[−2318,+∞[0\in \biggl[\dfrac{-23}{18}, +\infty\biggl[0∈[18−23,+∞[ donc 0 a un antécédent unique dans ]−∞,−23]\biggl]-\infty,-\dfrac{2}{3}\biggl]]−∞,−32]
L'équation g(x)=0 a donc une solution unique dans ]−∞,−23]\biggl]-\infty,-\dfrac{2}{3}\biggl]]−∞,−32]
Graphiquement, l'unique solution dans cet intervalle est l'abscisse de I2ème cas : x∈]−23,+23[x\in \biggl]\dfrac{-2}{3},+\dfrac{2}{3}\biggl[x∈]3−2,+32[
même principe.
Graphiquement, l'unique solution dans cet intervalle est l'abscisse de J3ème cas : x∈[23,+∞[x\in\biggl[\dfrac{2}{3},+\infty\biggl[x∈[32,+∞[
même principe.
Graphiquement, l'unique solution dans cet intervalle est l'abscisse de KD'ou la réponse demandée
Graphique relatif à g :
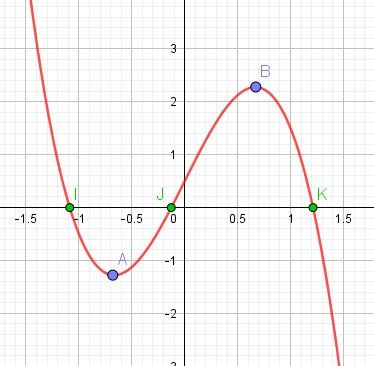
Remarque : Utiliser la fonction g pour étudier g(x)=0 est clair.
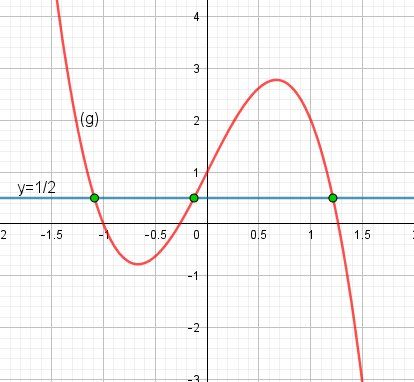
ll est bien sûr tout aussi possible de faire le même raisonnement en utilisant la fonction f pour étudier f(x)=1/2.
C'est une question de goût personnel...Graphique relatif à f :