Devoir maison sur l'aire et les fonctions

Bonjour
J'aimerais que vous m'aidiez SVP car je n'ai pas compris du tout

Notre prof donne les devoirs en avance, cette-à-dire qu'il nous donne des choses avant les expliquer

SVP ajoutez le plus de dètails possible

Merci d'avance

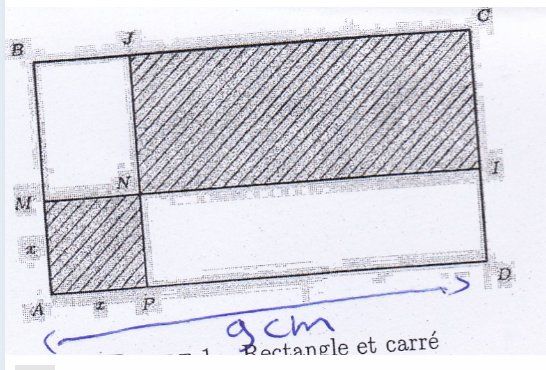
Soit (ABCD) un rectangle tel que AB = 5 centimbtres et AD = 9 centimbtres ; soit M un point quelconque du segment lAB. On construit le carre (AMNP) et Ie rectangle (NICJ) comme indique sur la figure ci-dessous'
On pose AM : x et on note
F(x) l'aire de la partie qui est hachuree.

Partie A : recherche du minimum de la fonction f.

determiner l'ensemble de definition de la fonction f.
demontrer que $f(x)=2x^2-14x+45$
A l'aide de votre calculatice, conjecturer le minimum de la fonction f, ainsi que la valeur de x pour laquelle il est atteint. (les valeurs etant arrondies 0.1 pres)

Partie B : resolution de l'inequation $f(x)≥25f(x)\ge25$ .
On cherche maintenant pour quelles valeurs de x l'aire hachuree est superieure a 25 centimetre carres, ce qui revient a resoudre l'inequation f(x)≥ 25.

Etablir que l'inequation se ramene $x2−7x+10≥0x^2-7x+10\ge 0$
Demontrer que $x^2-7x+10 = (x-2)(x-5$ ).
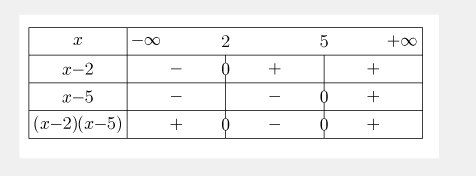
A l'aide d'un tableau de signes, répondre a la question posee

Bonsoir Prince-Of-Darkness,

Indique tes éléments de réponse et la question qui te pose problème.

L'aire de la partie hachurée : Aire du carré plus l'aire du rectangle, soit
$f(x) = x^2 + (9-x)(5-x)$

Partie A

C'est une fonction du second degré donc l'ensemble de définition est : .....
Développe l'expression de $f (x)$
Conjecture le minimum en utilisant le tableur de la calculatrice.

Partie B

Simplifie l'inéquation : $2x2−14x+45−25≥02x^2 - 14x + 45 - 25 \geq 0$
Factorise l'expression $x^2 - 7x +10$ ou développe l'expression $(x - 2) (x - 5)$
Construis un tableau de signe en prenant pour valeurs particulières de $x$ les valeurs qui annulent le polynôme, puis tu écris le signe de $(x - 2)$ , puis $(x - 5)$ puis du polynôme.

Indique tes résultats si tu souhaites une correction.

Bonjour,
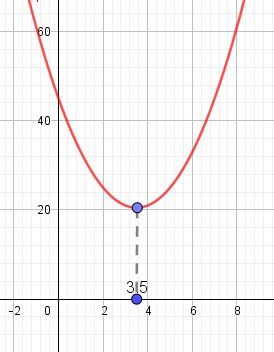
Quelques détails pour vérifier éventuellement les réponses à trouver.

A) Courbe (rectifiée) pour vérifier le minimum demandé

B) tableau de signes pour résoudre $\ge 25$ (à utiliser pour $x≥0x\ge 0$ et $x≤5x\le 5$ )

@mtschoon Merci ;D

@Noemi a dit dans Devoir maison sur l'aire et les fonctions :

C'est une fonction du second degré donc l'ensemble de définition est : .....

Merci beaucoup pour vouloir m'aider ;D

Remarque : ^2 = au carre ;D
mes reponses :
A)1)
Df = [0;5]
2) f(x) = l'aire de AMNP + l'aire de NICJ
= x^2+(9-x)(5-x)
= x^2+45-9x-5x+x^2
= 2x^2-14x+45
3) le minimum est egal a -7.5 et est atteint pour x=3.5

Corriger moi SVP

@mtschoon Pouvez-vous m'expliquer les methodes que vous avez fait pour obtenir cette courbe SVP ?
Merci d'avance

Bonjour Prince-Of-Darkness,

A

Le domaine de définition de la fonction est $R\mathbb{R}$ . Il n'y a pas de valeur interdite mais x varie de 0 à 5.
Vérifie le calcul pour le minimum, c'est bien pour $x = 3, 5$ et $f (3, 5) = . . . .$

@Noemi Il faut corriger ma reponse sur la question 1 de A ?
3) x=3.5 et f(3.5)=20.5

pour B)1)
2x^2-14x+45-25⩾0
2x^2-14x+20⩾0
(2(x^2-7x+10))/2⩾0/2
x^2-7x+10⩾0

2)(x-2)(x-5)= x^2-5x-2x+10
=x^2-7x+10
3) s=[-infinie;2[ U ]5;+infinie[

@Prince-Of-Darkness

Ta réponse est correcte pour le A 1.
B
1 et 2 juste
3 Tu construis le tableau de signes pour $x$ variant de 0 à 5
et la solution est comprise dans cet intervalle, donc rectifie la réponse.

@Prince-Of-Darkness

A) Pour faire la courbe, j'ai utilisé Geogebra (logiciel gratuit) mais tu peux obtenir la courbe sur ta calculette si elle est graphique.
La courbe donnée est la représentation graphique de $\fbox{f(x)=2x^2-14x+45}$ vu que c'était une aide à la question A).

Une remarque (pour B) : j'ai fait le tableau de variation pour $x∈Rx\in R$ , c'est à dire x variant de - $∞\infty$ à $+∞+\infty$ mais la condition de ton exercice est $x∈[0,5]x\in [0,5]$ , donc tu peux faire varier x seulement de 0 à 5.
Si tu préfères , tu peux faire le tableau de signe sur R, mais dans ta conclusion, tu restreins à [0,5]

@mtschoon Merci Monsieur.
Donc s= [0;2] U [5] ?

Dsl que je sois si nul en maths ;D

@Prince-Of-Darkness

C'est la solution.

$f (3, 5) = 20, 5$
C'est bien mtschoon a rectifié le graphe.

Donc pour conclure je peux dire que pour tous les nombres dans l'intervalle [0;2] + 5 l'aire hachuree est superieur a 25 ?

@Prince-Of-Darkness

Pour ta conclusion, tu peux effectivement mettre $x∈[0,2]∪x\in[0,2] \cup$ {5} (mets des accolades autour de 5 car il s'agit d'une valeur isolée.
Mais tu peux signaler que x=0 et x=5 sont des cas "limites" (regarde ce que ça donne sur ton schéma...)
Pour avoir véritablement deux zones hachurées, il faut prendre $x∈]0,2]x\in]0,2]$

Merci pour votre aide. C'etait tres utile. ;D

De rien @Prince-Of-Darkness ,

Tu as fait du bon travail !