Dm sur les fonctions

Bonjour j’ai un dm sur les fonctions j’ai un peu de mal a le faire, du moins j’aimerai etre sur de mes reponses avant de continuer. Nous venons de commencer le chapitre.
Énoncé:
On considere la fonction f definie sur R -{2}=]-l’infini;2[U]2;+l’infini[ par f(x)=(2x^2-3x-1)/x-2
On appelle Cf la courbe representative dans un repere orthonormal (0;i;j)
1-a) a l´aide d’un logiciel la courbe a été tracée
•Conjecturee les limites de f au bornes de son ensemble de définition
Mes réponses : en -l’infini la limite est -l’infini
En 2- la limite est -lninfini
En 2+ la limite est + l’infini
Et en + linfini est + l’infini
•Conjecturer le sens de variation de la fonction f sur son domaine de definition
La fonction semble etre croissante sur son domaine de definition
1-b) demontrer vos limites conjecturées et en deduire l’existence d’eventuelles asymptotes paralleles aux axes du repere.
Mes reponses : j’ai trouvé que les limites etaient coherentes avec celle conjecturees.
J’ai ensuite dis que lorsque x tendait vers -+ linfini il y avait 2 asymptotes d’equation y=2x et donc parallèles a l´axe des abcisses.
Lordque x tend vers 2 alors 2 asymptotes d’equation x=2 et paralleles a l´axe des ordonnes.
1-c) f’(x)= (2x^2-8x+7)/(x-2)^2
Deduire les variations de la fonction f sur son domaine de definition puis dressee le tableau de variation.
J’ai donc calculer f’(x)=0 soit le numerateur = 0 j’ai fais une equation du 2nd degré avec comme solution x1= (4-racine2)/2 et x2 = (4+racine2)/2
Puis j’ai dressé le tableau de signe avec + aux extrémités des 0 et - au milieu
J’ai ensuite fait le signe de (x-2)^2 qui s’annule lorsque x=2 et j’ai mis + a droite du 0 et - a gauche j’en ai ensuite deduis que la fonction f était croissante de -l’infini a 2 et de 2 a + l’infini
Or je pense avoir fait faux qlq part car en regardant le graphique ce n’est pas ce que j’aurait deduit
Merci d´avance si vous m’aidez

@shana67 ,

Une remarque lorsque tu écris des formules.
Si tu n'écris pas en Latex, mets suffisamment de parenthèses en éviter toute ambiguité.

Je suppose que tu parles de $f(x)=2x2−3x−1x−2f(x)=\dfrac{2x^2-3x-1}{x-2}$
Tu aurais dû écrire:
f(x)=2x^2-3x-1)/(x-2)

Je te joins la courbe avec les 2 asymptotes d'équations x=2 et y=2x+1

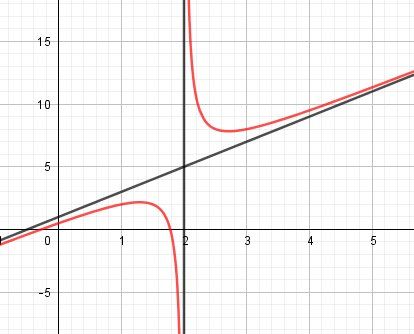
Je regarde tes réponses
1)a)Pour les limites : c'est bon

Le sens de variation que tu proposes n'est pas bon.
Pour x< 2, f est croissante puis décroissante
Pour x>2, f est décroissante puis croissante

1)b) En ce qui concerne les asymptotes, dans cette question, on te demande seulement les asymptotes éventuelles parallèles aux axes
Il y en a une seule , parallèle à l'axe des ordonnées, d'équation x=2

En + $∞\infty$ et- $∞\infty$ , il y a une asymptote oblique d'équation y=2x+1 que l'on ne te demande pas ( j'ignore si, avec ton cours, tu sais la trouver)

1)c) la dérivée est bonne et les valeurs qui l'annulent aussi.

Pour $x≠2x\ne 2$ , iL faut que tu trouves le signe du numérateur correctement (signe d'un polynôme du second degré)
(signe de a, signe de -a, signe de a)

Tu dois trouver un tableau de variation totalement conforme au graphique (sans oublier la double barre pour x=2).

@mtschoon
Lorsqu’on me demande les asymptotes paralleles aux axes du répère cela veut dire paralleles a l´axe des ordonnes ?

@shana67
asymptotes parallèles aux axes du répère veut dire : parallèle à l'axe des abscisses ou parallèle à l'axe des ordonnées.

Ici, tu as une asymptote parallèle à l'axe des ordonnées (x=2)

Il n'y a pas d'asymptote parallèle à l'axe des abscisses.

@mtschoon
Pourquoi je ne donne pas cele qui est d´equation y=2x

@shana67
EN ce qui concerne le tableau de signe et de variations j’ai reussi donc c’est bon.
EN revanche j’ai dautre question sur mon Dm que je n’arrive pas a faire du coup je fais un autre post ou je les met a la suite ?

@shana67

S'il s'agit de questions du même exercice, tu le mets ici.

S'il s'agit d'un autre exercice, tu ouvres une autre discussion.

@shana67 ,

Je n'avais pas vu t'a question relative à y=2x

y=2x n'est pas l'asymptote oblique. C'est faux
L'asymptote oblique est y=2x+1 (il faut bien sûr connaître une méthode pour pouvoir le justifier...)

Mais, en plus,dans cette question, l'énoncé ne te demande que les asymptotes éventuelles parallèles aux axes du repère, donc y=2x+1 n'est pas à donner ici car elle n'en fait pas partie.

@mtschoon
2) en utilisant votre calculatrice, il semblerait qu’en + l’infini et en - l’infini la courbe Cf se rapproche d’une droite D non parallele aux axes du reperes. Le but de cet exercice es de determiner D et de justifier cette observation.
2-a) determiner les reels a,b, c tels que pour tout reel x different de 2
F(x)=ax+b+c/(x-2)
Mes reponses :
J’ai pensé a faire l’identificAtion
Ainsi j'obtiens
2x^2-3x-1/(x-2) = ax^2-2(ax+b)+bx+c/(x-2)
Par identification j’obtiens
a= 2
b = -3
c = -1
ax+b=0
Mais la je bloque
2-b) on considere alors la droite D d’equation y=2x+1. Etudier les positions relatives de D Et cf
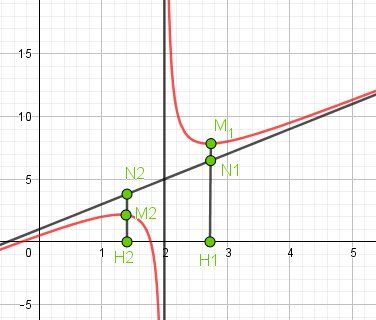
2-c) soit x un reel different de 2 on appelle M et N les points d’abscisses x et situés respectivement sur cf et D. Exprimer la distance MN en fonction de x suivant les valeurs de x
2-d) determiner les limites de la fonctions x—> MN en + l’infini et - l´infini et interpreter graphiquement les résultats

@shana67

Et bien, voilà. Elle arrive l'asymptote oblique.

Cette question est faite pour te faire trouver l'asymptote oblique (qui sera d'équation y=2x+1, à la fin de la démonstration)

C'est bien la méthode par identification.
Revois tes calculs.

$ax+b+cx−2=(ax+b)(x−2)+cx−2ax+b+\dfrac{c}{x-2}=\dfrac{(ax+b)(x-2)+c}{x-2}$

Pour tout x différent de 2
$ax+b)(x-2)+c=2x^2-3x-1$
Tu développes le membre de gauche , tu le mets sous forme d'un polynôme du second degré et tu identifies au membre de droite.

Tu dois trouver a=2, b=1, c=1
d'où
$\fbox{f(x)=2x+1+\dfrac{1}{x-2}}$

IL faut que tu obtiennes ça; les questions suivantes en sont les conséquences.
Donne tes calculs si tu trouves pas ton erreur.

@mtschoon
Je ne comprend pas comment vous avez fait pour trouver b et c

@shana67
Je viens de t'indiquer la méthode.

J'explicite un peu

$ax+b)(x-2)=2x^2-3x-1$

Après développement et regroupement:
$ax^2+x(-2a+b)+c=2x^2-3x-1$

Identification :

${a=2−2a+b=−3c−2b=−1\begin{cases}a=2\cr-2a+b=-3\cr c-2b=-1\end{cases}$

Tu résous ce système pour trouver a, b, c.

@mtschoon
D’accord merci je vais reprendre ca

Oui, et reposte si besoin.

Si tu as besoin d'un exemple traité pour comprendre la méthode, tu peux regarder ici :
http://tanopah.jo.free.fr/ADS/bloc1/polyfct4i.html

@mtschoon
Re bonsoir je voulais juste savoir pourquoi on peut ecrire 2x^2-3x-1=(ax+b)(x-2)+c ?
Pourquoi on retire la fraction (je sais que c’est plus simple pour calculer mais je voudrais quand meme comprendre svp

@mtschoon
Concernant la question sur les positions relatives
J’ai trouvé que f(x)-y=1/(x-2)
J’ai ensuite dressé le tableau de variation ce qui m´a donne
Sur ]- l’infini;2[ Cf est en en dessous de D
Sur ]2;+ l’infini[ Cf est au dessus de D

En revanche je ne suis pas sur car j’avais un doute sur le signe de la fonction inverse
Je sais que c’est negatif de -l’infini a 0 puis positif de 0 a + l´infini mais pour cette exo je doute

@shana67

Pour répondre à la question $2x^2-3x-1=(ax+b)(x-2)+c$ :

Tu a, pour $x≠2x\ne 2$ , $(ax+b)(x−2)+cx−2=2x2−3x−1x−2\dfrac{(ax+b)(x-2)+c}{x-2}=\dfrac{2x^2-3x-1}{x-2}$
Les dénominateurs étant égaux, comme les quotients sont égaux, les numérateurs sont nécessairement égaux

IDEE : Pour $B≠0B\ne 0$ $AB=CB\dfrac{A}{B}=\dfrac{C}{B}$ <=> $A = C$

( Tu peux voir ou revoir la méthode avec le lien que je t'ai indiqué )

Pour le 2)b) tes conclusions sont bonnes

Pour x >2, x-2 >0 donc 1/(x-2) >0 donc f(x) > y donc (C) au dessus de( D)
Pour x <2, x-2 <0 donc 1/(x-2) <0 donc f(x) < y donc (C) en dessous de (D)

Pour les deux dernières lignes de ton message, explique de quoi tu parles, ce n'est pas clair.

@mtschoon
D’accord je comprend mieux maintenant merci beaucoup.
Concernant les 2 dernieres lignes ce n’est pas important vous y avez répondu indirectement

@mtschoon
Pour la suite de l’exercice, les 2 dernieres questions, je ne sais ps trop comment faire
Pour l’avant derniere je pensais utiliser la formule d’une longueur mais on ne connait pas les coordonnes des points M et N

@shana67 ,

Pour toute valeur de x différente de 2, l'ordonnée de M est f(x) et l'ordonnée de N est y=2x+1

$M (x, f (x)$ ) et $N (x, 2 x + 1)$

Tu peux utiliser la formule de la distance, mais tu peux raisonner encore plus simplement en calculant cette distance avec le graphique
Tu as deux cas à voir : x < 2 et x > 2

@mtschoon

Je vous avoue que je ne vois vraiment pas comment faire ..

@shana67 ,

Le plus simple est, sur le schéma, pour une valeur de x quelconque, de placer M et N.
Tu constateras que la distance MN et la différence des ordonnées de M et N
Une distance est un nombre positif

Pour x > 2, (C) est au dessus de (D) ; M est au dessus de N

$MN=f(x)-(2x+1)=\fbox{\dfrac{1}{x-2}}$

Tu étudies maintenant le cas x < 2

@shana67 ,

schéma pour aider

@mtschoon
Pour x<2 Cf est en dessous de D donc N est au dessus de M
Mais par le calcul c’est la meme chose non?

@mtschoon
Je dois conclure que la longueur MN = 1/(x-2) ?

@shana67 , il faut faire attention au signe.

Comme tu l'indiques, pour x < 2, N est au dessus de M

La distance MN (qui doit être positive), est donc :

$MN=(2x-1)-f(x)=-\dfrac{1}{x-2}=\dfrac{-1}{x-2}=\fbox{\dfrac{1}{2-x}}$

Si tu voulais concentrer les deux cas (x > 2 et x < 2) en une seul, tu pourrais écrire avec des valeurs absolues :
$\fbox{MN=\dfrac{1}{|x-2|}}$ mais cela ne semble pas être demandé.

@mtschoon
D’accord donc MN lorsque x>2 MN = 1/(x-2) et lorsque x<2 MN= -1/(x-2)
Je conclus de cette facon la ? Car comme vous le dites une longueur doit etre positive du coup je fais comment pour bien repondre a la consigne

@shana67

L'énoncé indique : "Exprimer la distance MN en fonction de x suivant les valeurs de x"
Donc, répondre avec les deux cas (x<2 et x > 2) est ce qui ést attendu.

@mtschoon
D’accord merci bcp
Et concernant la derniere question sur les limites
x—-> MN en + et - l’infini
Pour x<2
Lim MN soit -1/(x-2)quand x tend vers + l’infini = 0
Lim MN soit -1/(x-2)quand x tend vers - l’infini = 0
Pour x>2
Lim MN 1/(x-2)quand x tend vers + ou - l’infini
= 0

On peut donc interpreter cela en disant que à partir d’une certaine valeur la distance entre la droite et la courbe sera nulle ?

@shana67 ,

L'idée est bonne, mais fait attention.

Pour la limite de MN lorsque x tend vers + $∞\infty$ ,
tu dois prendre seulement l'expression de MN valable pour x > 2

Pour la limite de MN lorsque x tend vers - $∞\infty$ ,
tu dois prendre seulement l'expression de MN valable pour x < 2

Dans les deux cas la limite de MN est 0, donc en + $∞\infty$ et - $∞\infty$ la droite (D) s'approche indéfiniment de la courbe (C), sans la toucher :
(D) est asymptote à (C)

@mtschoon
On peut dire que c’est une asymptote horizontale?

@shana67

"horizontale" veut dire "parallèle à l'axe des abscisses" c'est à dire d'équation de la forme y=constance.

Tu trouves que y=2x+1 est dans ce cas ?

Il y a 3 types de droites asymptotes à une courbe

$x = a$ asymptote "verticale" (parallèle à y'y)
$y = b$ asymptote "horizontale" (parallèle à 'x'x)
$y = a x + b$ (avec $a≠0a\ne 0$ ) asymptote "oblique"

Tire la conclusion sur y=2x+1

@mtschoon
D’accord je ne savais pas
Y=2x+1 est une asymptote oblique
(Je n’ai pas encore étudiée les asymptotes obliques)

@shana67 ,
Maintenant, ta conclusion est la bonne.

Je pense que la dernière partie de ton exercice est une introduction à ces asymptotes dites obliques.
Si tu ne connais pas encore le terme, tu peux parler seulement d'asymptote ( ni verticale , ni horizontale).

Je t'indique un lien pour consultation éventuelle sur ces asymptotes obliques (en attendant que ton professeur te l'explique en cours)
https://www.youtube.com/watch?v=55JnpXFW0_4

@mtschoon
D’accord merci beaucoup pour toute votre aide
Bonne journee

De rien @shana67

Si tu as un peu de temps, je te conseille de refaire seul(e) tout l'exercice pour être sûr(e) de tout maîtriser.

Bonne semaine !

@mtschoon
Oui c’est ce que je comptais faire tout de suite d’ailleurs

@shana67

C'est très bien !