Prix de Bijoux à trouver
-
Nnovicemaths6eme dernière édition par mtschoon
Bonjour,
Je suis bloquée dans l’aide que je peux apporter à mon enfant, élève de 6ème.
Je ne trouve pas de sujet similaire sur le forum.
Elle ne comprend pas comment aborder l’exercice et moi non plus.
Elle a 3 carrés avec des triangles à l’intérieur :
1/ bijou à 11€ avec 4 triangles verts et 4 blancs
2/ bijou à 9,10€ avec 2 triangles vertes et 6 blancs
3/ bijou à ? Avec 3 triangles verts et 5 blancs.
Il faut trouver le prix du bijou 3.
Elle a cherché les multiples en commun, divisé le nombre de cases blanches pas vertes et le contraire.
Je bloque sur la décimale. Je ne sais pas non plus comment la conseiller pour prendre le problème.
Quelqu’un pourrait l’aiguiller s’il vous plaît ?
(Exercice 115 page 54 du manuel dimension maths de 6eme. Hatier)
Grand merci à vous par avance
Bonne journée  url de l'image))))))))
url de l'image))))))))
-
mtschoon dernière édition par mtschoon

@novicemaths6eme , bonjour,
Je pense que des données écrites dans l'énoncé n'ont pas été recopiées ici, car sinon l'exercice n'est pas faisable...
Les triangles verts ont-ils le même prix?
Les triangles blancs ont-ils le même prix?
Merci de compléter l'énoncé.
-
Bonjour novicemaths6eme,
Si on considère que le prix correspond aux nombres de triangles verts et blancs et que pour chaque bijoux, le prix d'un triangle vert est fixe et identique ainsi que le prix d'un triangle blanc.
En comparant le nombre total de triangles blancs et verts des bijou 1 et 2 avec le nombre de triangles blanc et vert du bijou 3, on peut en déduire le prix du bijou 3.
-
mtschoon dernière édition par mtschoon

@Noemi et @novicemaths6eme , bonjour,
@novicemaths6eme , suis les pistes de Noemi ( en suppose bien sûr que les précisions utiles soient indiquées dans l'énoncé)
Evidemment, en 3ème, il aurait été facile de traiter cet exercice avec plus de rigueur...
Piste pour démarrer , les expressions étant des valeurs en euros
Bijou 1 : 4 verts +4 blancs=11
Si besoin pour la suite, on peut déduire que :
1 vert+1 blanc=11/4=2.75
2 verts +2 blancs=2.75 x 2=5.50Bijou 2 : 2 verts +6 blancs=9.10
en décomposant pour pouvoir utiliser les résultats obtenus avec le bijou 1
(2 verts +2 blancs)+4 blancs= 5.50 +4 blancs=.10on peut déduire la valeur de 4 blancs puis de 1 blanc
Vu que 1 vert+1 blanc=2.75,
on peut déduire la valeur de 1 vertConséquence : on utilise les réponses obtenues pour 1 blanc et pour 1 vert, pour trouver de prix du bijou 3
@novicemaths6eme , tu peux donner tes réponses si tu as besoin d'une vérification.
-
Nnovicemaths6eme dernière édition par
@mtschoon @Noemi
Merci beaucoup. Je pense que c'est le seul raisonnement possible en effet.
Ma fille a tous ses cahiers et manuel. Il n'y a rien d'autre comme complément d'énoncé.
Votre aide l'a beaucoup aidée. Elle a juste pris le raisonnement pour le bijou 1 et fait tout le reste. Elle trouve 10,05 pour le bijou 3.
Verdict demain.
Je vous tiens au courant ! Bonne soirée
-
La réponse est bien 10,05 €.
-
mtschoon dernière édition par mtschoon

Cet énoncé est une reprise d'un exercice du Brevet 2011.
Les triangles étaient en verre ou métal au lieu de blanc ou vert.
Je joins l'énoncé du Brevet trouvé sur le web.
Dans le schéma joint, le métal gris est plutôt bleuté...Dans l'énoncé du brevet, il était bien indiqué
"Tous les triangles en métal ont le même prix.
Tous les triangles en verre ont le même prix"
Cela aurait dû être indiqué ici...
IL fallait donc l'admettre pour pouvoir faire les calculs demandés...
Les calculs ont été bien faits vu que le résultat est exact .C'est l'essentiel.Enoncé du brevet:
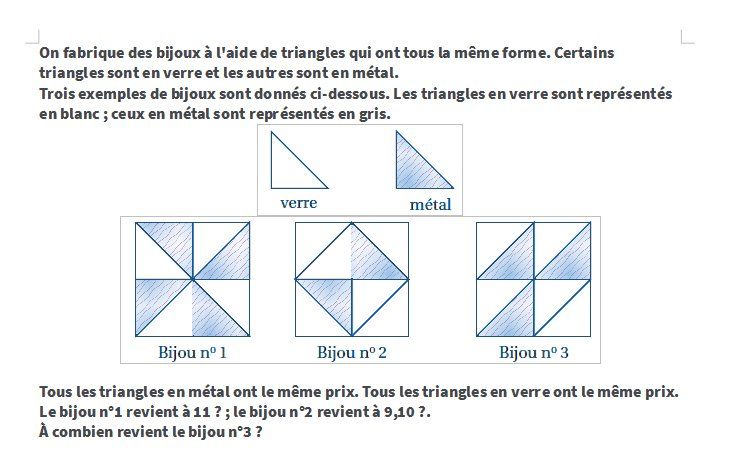
Bonne journée !
-
Nnovicemaths6eme dernière édition par
@mtschoon
J'avoue être étonnée de voir un exercice de brevet, avec énoncé incomplet (le professeur l'a admis), donné à des élèves de 6ème. Encore merci. Ma fille était soulagée.
-
mtschoon dernière édition par mtschoon

De rien @novicemaths6eme
Si votre fille à compris, c'est parfait.
Et si un jour elle a besoin, nous l'aiderons au mieux (si elle le souhaite).Bonne soirée !
-
CCandiice dernière édition par
Je pense que la meilleure chose à faire c'est d'acheter les bijoux et de ne plus en parler ! lol