AIDE!!! PROB CONDITIONELLE ARBRE
-
Sasouno dernière édition par
Bonjour, j'arrive pas a faire l'arbre pondéré dans un exercice
L'exercice:
Une urne A contient 4 jetons rouges et 6 jetons noirs. Une urne B contient 1 jeton rouge et 9 noirs.Partie 1:
Un joueur dispose d'un dé à 6 faces, non truqué, numérotées de 1 à 6.Il le lance.S'il obtient 1, il tire un jeton de l'urne A, sinon il tire un jeton de l'urne B. Il gagne si le jetons tiré est rouge.- représente la situation décrite parun arbre pondéré
- Calculet la prob pour que le jeton provienne de A et soit rouge.
- Prouver queP(R)= 0,15
- Si le joueur a gagné, la prob pour que le jeton provienne de l'urne A est-elle supérieure a la prob pour qu'elle provienne de l'urne B? Justfiez vos reponse par calcul.
Je suis vraiment perdu je sais pas comment répondre à ces questions
-
Bonjour Sasouno,
Pour l'arbre pondéré,
au début : jet du dé, deux possibilités soit 1 (P(1) = 1/6), soit 2,3,4,5,6 (P(non1) = 5/6)
puis si 1 urne et deux possibilités soit jeton rouge (P(R) = ....) soit jeton noir (P(N) = ...)
Si non 1, deux possibilités .....indique tes éléments de réponse si tu souhaites une correction
-
L'arbre pondéré
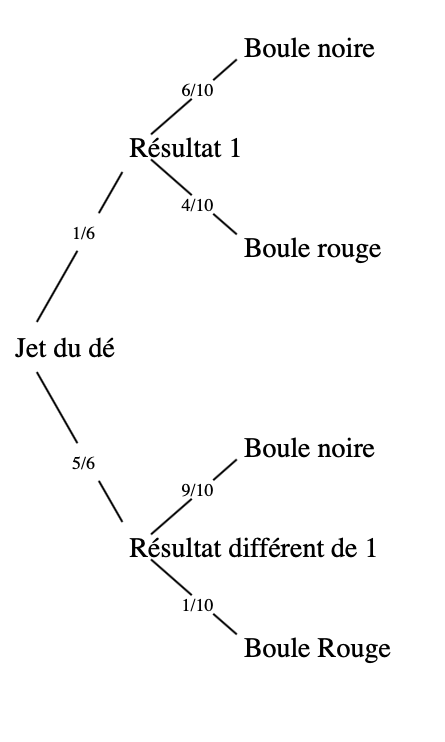
-
mtschoon dernière édition par mtschoon

Bonjour,
Il semble que Sasouno n'ai pas eu besoin d'aide pour pour les conséquences de l'arbre probabiliste,
Quelques éléments pour consultation éventuelle.
Notations :
Soit A l'évènement : la face 1 est obtenue et un jeton de A est tiré
Soit B l'évènement la face 2 ou 3 ou 4 ou 5 ou 6 est obtenue et un jeton de B est tiré
Soir R le jeton tiré est rouge
Soit N le jeton tiré est noir.$\fbox{p(A\cap R)}=\dfrac{1}{6}\times \dfrac{4}{10}$
On compte$\fbox{p(R)=p(A\cap R)+p(B\cap R)}=(\dfrac{1}{6}\times \dfrac{4}{10})+(\dfrac{5}{6}\times \dfrac{1}{10})$
On compteProbabilités conditionnelles sachant R
$\fbox{p_R(A)=\dfrac{p(R\cap A)}{p(R)}}$
On compte en utilisant les résultats précédents.$\fbox{p_R(B)=\dfrac{p(R\cap B)}{p(R)}}$
Même principe.