second degré et droite

[pouvens]

bonjour vous pouvez m'aider svp
un objet est jeté en l'air , à l'instant t=0 , à la vitesse initiale de 20 m/s (m/s -1 ). Sa hauteur h à un instant t est donnée par la formule : h(t)=-5t²+20t+5
(t étant exprimé en seconde et h en mètres )
Le but de cet exercice est de déterminer la hauteur maximale de l'objet ,et, au bout de combien de temps , cet objet touche le sol.

1. montrer que h(t)=-5(t-2)²+25
2. tracer la courbe de cette fonction sur l'intervalle [0;5]. ( donner le tableau de valeur )
3. donner le tableau de variations de cette fonction .
   En déduire : (compléter avec <ou>): h(1) .......... h(2)............... h(3)..................... h(4)........
4. a quel instant la hauteur de l'objet est elle maximale , et quelle est cette hauteur?
5. calculer à quel instant cet objet touche t-il le sol ?
6. Résoudre graphiquement l'inéquation : h(t) ≥20, puis retrouver les par le calcul
   donner l'interprétation concrète de cette inéquation
7. pour x ∈[0;5], alors h(x)∈...............

[Noemi]

Bonsoir pouvens,

Indique tes éléments de réponse et la question qui te pose problème.

1. Soit tu factorises $h(t)$, soit tu développes l'expression au carré.
2. Fais un tableau de valeurs, tu peux utiliser un pas de 1 et trace la courbe. Utilise ta calculatrice pour vérifier le résultat.
3. Dresse le tableau de variations.
4. Fais une lecture du tableau de variations.
5. Résous $h(t)=0$.
6. Trace la droite d'équation $y=20$ et résous l'inéquation.

[pouvens]

1. (-5*t)²

[Noemi]

@pouvens

Développe $(t-2{)}^2$ en utilisant les identités remarquables.

[pouvens]

t²-4t+4 comme ça

[Noemi]

@pouvens

Oui,

Calcule maintenant $-5(t-2{)}^2+25$

[pouvens]

dsl j'ai pas compris

[Noemi]

@pouvens
C'est la question 1.
$h(t)=-5(t-2{)}^2+25=-5(t^2-4t+4)+25$
Développe la parenthèse et simplifie

[pouvens]

-5t²-20t-20+25=-5t²-20t+5

[Noemi]

@pouvens

une erreur de signes.
$h(t)=-5(t-2{)}^2+25=-5(t^2-4t+4)+25$
$h(t)=-5t^2+20t-20+25=-5t^2+20t+5$

[pouvens]

ok merci

[Noemi]

@pouvens

Fais le tableau de valeurs.

[pouvens]

j'ai pas compris pour la 2

[Noemi]

@pouvens

Construis un tableau de valeurs
$x$ varie de 0 à 5 choisis un pas de 1,
Soit pour $x$ 0 ; 1 ; 2 ; ......

[pouvens]

d'accord merci c'est bon

[pouvens]

x 0 1 2 3 4 5
f(x) 5 20 25 20 5 -25

en haut les x et en bas les f(x) dans l'ordre f(0)= 5 de suite en suite

[Noemi]

@pouvens

Une erreur pour $x=5$, $f(x)=-20$.

[pouvens]

@Noemi a dit dans second degré et droites :

−5t2+20t+5

ok merci je fais comment après svp

[Noemi]

@pouvens

Tu traces un repère et tu places les points du tableau de valeurs.

[pouvens]

oui après svp

[Noemi]

@pouvens

Si tu as tracé la courbe, dresse le tableau de variations.

[pouvens]

pour la courbe j'ai une parabole à l'envers après j'y arrive pas

[Noemi]

@pouvens

Pour le tableau de variations :
Quand $x$ varie de 0 à 2, $f(x)$ varie de 5 à 25, donc la fonction est croissante.
quand $x$ varie de 2 à 5, $f(x)$ varie de 25 à -20 donc la fonction est décroissante.
Tu dresses le tableau de variation correspondant.

[pouvens]

x 0 2 5

f(x) 5 / 25 ∖ - 20

[Noemi]

@pouvens

C'est correct à condition de mettre des flèches pour indiquer fonction croissante puis décroissante.

(compléter avec <ou>): h(1) < h(2)............... h(3)..................... h(4)........

[pouvens]

@Noemi
h(1)<h(2)
h(3)>h(4)

[Noemi]

@pouvens

Oui

et h(2) avec h(3) ?

[pouvens]

@Noemi
h(2)<h(3)

[Noemi]

@pouvens

Non,

h(2) > h(3)

Bonne nuit.

[pouvens]

@Noemi ok merci à vous aussi

[pouvens]

t=2 la hauteur est max et vaut 25m

[Noemi]

@pouvens

Oui n'oublies pas l'unité pour le temps, t = 2 s.

[pouvens]

@Noemi a dit dans second degré et droite :

−5t2+20t+5

5. −5t²+20t+5=0
   je fais comment

[Noemi]

@pouvens
Tu peux utiliser l'autre écriture de $h(t)$
$h(t)=-5(t-2{)}^2+25$
$h(t)=0$; $-5(t-2{)}^2+25=0$
$-5[(t-2{)}^2-5]=0$
$(t-2{)}^2-5=0$ en factorisant
$(t-2-\sqrt{5})(t-2+\sqrt{5})=0$
Calcules les valeurs de t puis indique celle qui correspond à la situation.

[pouvens]

t=2+√5
un truc comme ça

[Noemi]

@pouvens

Oui c'est la réponse, l'autre valeur de $t$ est négative.

Pour la question 6, utilise utilise aussi la deuxième écriture de $h(t)$.

[pouvens]

@Noemi a dit dans second degré et droite :

Oui c'est la réponse, l'autre valeur de ttt est négative.

je justifie comment

[Noemi]

@pouvens

De quelle question parles tu ?

[pouvens]

la 5
−5(t−2) ²+25≥ 0
−5[(t−2) ² −5] ≥ 0
(t−2) ²−5 ≥ 0

[Noemi]

@pouvens

La question 5 c'est $h(t)=0$
La question 6 c'est $h(t)\ge 20$
Soit $-5(t-2{)}^2+25\ge 20$
ou
$-5(t-2{)}^2+5\ge 0$
$-5[(t-2{)}^2-1]\ge 0$

Factorise l'expression entre les crochets.

[pouvens]

(t-2-√5)(t-2+√5)≥0

[Noemi]

@pouvens

Non,
$-5[(t-2{)}^2-1]\ge 0$ équivalent à
$(t-2{)}^2-1\le 0$

factorise

[pouvens]

je sais pas

[Noemi]

@pouvens

Je l'ai fait pour la résolution de l'équation.

$(t-2{)}^2-1\le 0$
$(t-2-1)(t-2+1)\le 0$

Simplifie puis fais un tableau de signes

[pouvens]

t=3 ou t=1
[1;3]

[Noemi]

@pouvens

C'est correct.

[pouvens]

ok comment donner l'interprétation
et la 7 je n'y arrive pas

[Noemi]

@pouvens

Pour l'interprétation. Pour un temps t variant de 1s à 3s l'objet est à une hauteur supérieure ou égale à 20 m.

Pour la question 7, quelle est la hauteur minimale et la hauteur maximale ?
Tu en déduis l'intervalle pour $h(t)$.

[pouvens]

[1;3] je sais pas si c' bon

[Noemi]

@pouvens

C'est la hauteur que l'on demande, pas le temps.
Hauteur minimale : ....
Hauteur maximale : ....

[pouvens]

Hauteur minimale :0 et Hauteur maximale : 5

[Noemi]

@pouvens

La hauteur correspond à $f(x)$, donc de 0 à 25 m.

[pouvens]

Hauteur minimale :0 et Hauteur maximale : 25

[Noemi]

@pouvens

Oui c'est correct.

[pouvens]

h(x)appartient [0;25]

[Noemi]

@pouvens

non,

$h(x)\in [-20;25]$

[mtschoon]

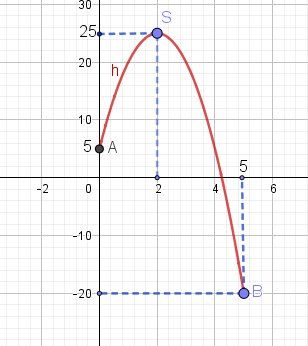
Bonjour,

Pour éclairer cette discussion, je joins la représentation graphique de h pour $t\in [0,5]$