équations et inéquations

Bonjour aidez moi svp
(x-2)(3-5x)≥ (8+7x)(x-2)

@pouvens , bonsoir,

C'est un peu tard, je te mets seulement une piste

Tu transposes :
$\ge 0$

Tu mets (x-2) en facteur :
$(x−2)[(3−5x)−(8+7x)]≥0(x-2)[(3-5x)-(8+7x)]\ge 0$

Tu simplifies la quantité entre crochets
$(x−2)[3−5x−8−7x]≥0(x-2)[3-5x-8-7x]\ge 0$
$\ge 0$

Tu fais un tableau de signes pour trouver le signe du produit $(x - 2) (- 12 x - 5)$ et tirer la conclusion.

Reposte si tu n'y arrives pas ou si tu veux une vérification.

Bonsoir.

@pouvens ,

Si tu as des difficultés pour étudier le signe d'un produit, tu peux suivre le lien ici ( paragraphe III pour étude de signe d'un produit avec tableau)
https://www.mathforu.com/seconde/factorisation-et-etude-de-signes-en-2nd/

Lorsque tu auras compris, fais le tableau relatif à ton exercice
Pour que tu puisses vérifier le tien, je te donne le tableau que tu dois trouver

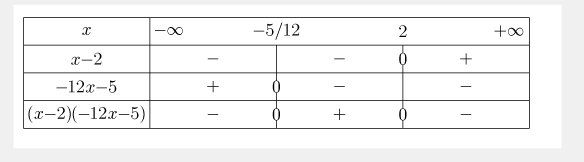
Tu pourras ainsi en déduire sur quel intervalle (pour x) le produit est positif (signe + dans le tableau).

Reposte si tu n'arrives pas à réaliser cela.

j'ai trouvé [-5/12;2]

@pouvens

C'est correct.

@pouvens ,
Comme te l'a indiqué Noemi, ta réponse est exacte.
J'espère que tu as compris le tableau de signes que je t'ai donné.
Je te conseille de refaire l'exercice seul(e) pour être sûr(e) de bien le maîtriser.

@mtschoon
D accord merci