Fonction polynôme du second degré
-
Ppouvens dernière édition par mtschoon
bonjour aidez moi svp
soit la fonction f(x) = x²-6x+5 définie sur R- montrer que f(x) =(x-3)²-4
- montrer que f(x) =(x-5)(x-1)
- en utilisant la forme appropriée de f , répondre aux questions suivantes:
a) donner les coordonnées du sommet de la courbe de f comment s'appelle cette courbe?
b) donner les coordonnées des points d'intersection de la courbe de f avec l'axe des abscisses
c) donner le tableau de variation de f sur R
d) donner l'équation de l'axe de symétrie de la courbe de f
e) montrer que f admet un minimum , puis donner le minimum de la fonction f sur R
f) calculer f(0) ; f(1) ; f(-3)
g) résoudre dans R l'inéquation f(x)<0
-
Bonsoir pouvens
-
Utilise le fait que (x−3)2=x2−6x+9(x-3)^2 =x^2 - 6x + 9(x−3)2=x2−6x+9
Donc f(x)=x2−6x+5+4−4=......f(x) = x^2 - 6x + 5 + 4 - 4 = ......f(x)=x2−6x+5+4−4=...... -
Utilise l'identité remarquable a2−b2=(a−b)(a+b)a^2 - b^2 = (a-b)(a+b)a2−b2=(a−b)(a+b)
-
a) Sommet pour x=3x= 3x=3 soit y=....y = ....y=....
b) Intersection avec l'axe des abscisses : y=0y = 0y=0
c) Tableau de variations
-
-
Ppouvens dernière édition par
@Noemi 3) y=9
-
Non
f(3)=(3−3)2−4=......f(3) = (3-3)^2 - 4 = ......f(3)=(3−3)2−4=......
-
Ppouvens dernière édition par
@Noemi
y=-4
-
Oui
-
Ppouvens dernière édition par
@Noemi
Ok merci et après
-
Indique tes réponses pour 3. b), c), .....
-
Ppouvens dernière édition par
@Noemi a dit dans Fonction polynôme du second degré :
Utilise l'identité remarquable a2−b2=(a−b)(a+b)a^2 - b^2 = (a-b)(a+b)a2−b2=(a−b)(a+b)
f(x) =(x-5)(x-1) c'est possible ça
-
Oui c'est possible, utilise l'identité remarquable que j'ai indiquée.
a=x−3a = x- 3a=x−3 et b=2b = 2b=2
-
Ppouvens dernière édition par
(x-3-2) (x+3+2)
-
Une erreur de signe.
c'est (x-3-2)(x-3+2)
Simplifie
-
Ppouvens dernière édition par
(x-5)(x-1)
-
-
Ppouvens dernière édition par
je sais pas comment faire
-
Suis les indications que j'ai indiquées dans mon premier message.
-
Ppouvens dernière édition par
@Noemi a dit dans Fonction polynôme du second degré :
b) Intersection avec l'axe des abscisses : y=0
x=-4
-
3 a) Le sommet est atteint pour x=3x = 3x=3, calcule f(3)f(3)f(3) pour obtenir l'ordonnée du sommet.
-
Ppouvens dernière édition par
f(3)=(3−3) ²-4=-4
x=3 y=-4
-
@pouvens
OuiPour la question b) résous f(x)=0f(x)=0f(x)=0.
-
Ppouvens dernière édition par
x²-6x+5 =0
x²-6x=-5
-
Utilise la forme factorisée :
(x−5)(x−1)=0(x-5)(x-1) = 0(x−5)(x−1)=0
si x−5=0x-5 = 0x−5=0, soit x=.....x = .....x=.....
ou
x−1=0x-1 = 0x−1=0, soit x=....x = ....x=....
-
Ppouvens dernière édition par
x=1 ou x=5
-
Ppouvens dernière édition par
x=1 ou x=5
-
Ppouvens dernière édition par
b) On déduit de la forme f(x) = (x-5)(x-1) que les racines du polynômes sont 5 et 1.Les coordonnées des points d'intersection de la courbe avec l'axe des abscisses sont (1 ; 0) et (5 ; 0)
c) f(x) est décroissante sur ]-∞ ; 3] et croissante sur [3 ; +∞[
d) L'abscisse du sommet de la courbe étant 3 , l'axe de symétrie de la courbe de f a pour équation x = 3
e)f(x) = x² - 6x +5 ; le coefficient a du polynôme est positive (a = 1) donc la parabole est tournée vers le haut.Son sommet est donc un minimum
Ce minimum est f(3) = 4
f) f(0) = 0² -6×0 +5 =5
f(1) = 0
f(-3) = 32
-
-
Ppouvens dernière édition par
d'accord et pour la g
-
Tu résous l'inéquation (x−5)(x−1)<0(x-5)(x-1)\lt0(x−5)(x−1)<0
Tu appliques la même démarche que dans l'autre exercice.
-
Ppouvens dernière édition par
]1;5[ c'est bon
-
C'est correct.
-
Ppouvens dernière édition par
-
-
Ppouvens dernière édition par
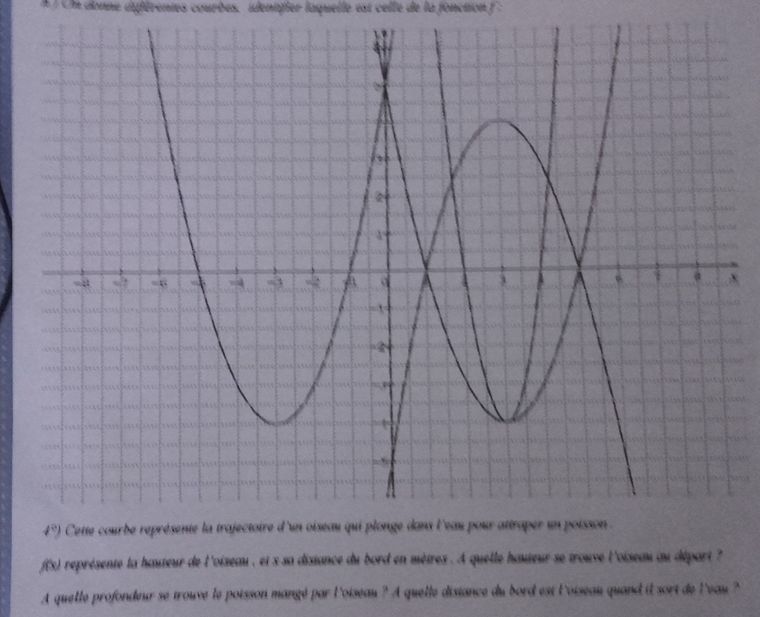
celui à droite avec le sommet vers le bas et qui coupe l'axe des abscisses à 1 et 5
-
Ou est placé l'oiseau ? le poisson ?
-
Ppouvens dernière édition par
l'oiseau est sur l'axe des ordonnées et le poison sur le sommet de la courbe
-
Donc indique la hauteur pour l'oiseau et la profondeur pour le poisson.
-
Ppouvens dernière édition par
l'oiseau = 5
poisson = -4 m
-
C'est correct.
-
Ppouvens dernière édition par
donc au départ l'oiseau se trouve à 5 m
et le poisson se trouve à -4 m
après l'autre question je ne comprends pas
-
On demande la valeur de xxx si y=0y = 0y=0.
-
Ppouvens dernière édition par
bein x=1;5
mais comment justifiez ça
-
C'est une lecture graphique x=5x = 5x=5.
-
Ppouvens dernière édition par
donc il se trouve à 5 m du bord
-
Oui si on suppose que l'axe des ordonnées est le bord.
-
Ppouvens dernière édition par
ok merci