DM repere orthonormé et fonctions

Bonjour

J'ai besoin de votre aide SVP

Le DM :
Le chemin le plus rapide.
Une personne est dans un bateau pneumatique, sur un lac. Il est assez loin de la rive, et remarque que la nuit commence à tomber. ElIe veut donc rentrer le plus vite possible chez elle, et doit d'abord rendre son embarcation la botique de location.

sur la figure ci-dessous, munie d'un repere orthonome R(O,I,J), la berge est representee par l'axe (OB), la boutique de location se trouve em B et la personne se trouve en A au debut du probleme. C est un point du segment [OB].
On choisit 1hm=100 m comme unite de longueur. Les points A et B sont definis par A(0,-5) et B(12,0).
Le parcours de ka oersonne se decompose en deux parties. Elle va, en ramant en ligne droite, du point A au point C. Puis elle marche en tirant son embarcation du point C au point B.
Sur le lac, la pesonne rame la vitesse 1/3 de hm/min. Le long de berge, elle marche en tirant son bateau 0,5 hm/min.

L'objet du probleme est de determiner la position que doit avoir le point C pour que la duree du parcours de la personne soit la plus petite possible.

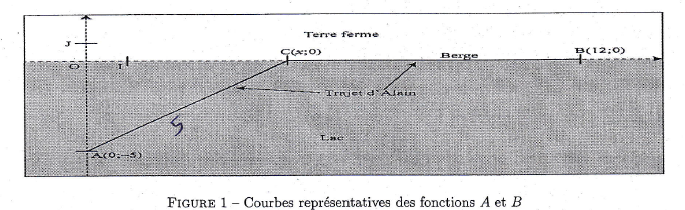
Partie A : Etude d'exemples.
l-. Dans cette question, on considere que C est l'origine du repere. C(0;0). Determiner dans ce cas Ia longueur
AC,la longueur CB.
Calculer alors la duree du trajet de la personne (en minutes).
2. Calculer la longueur du trajet si la personne va en B directement, c'est-a-dire si C(12,0).
Determiner alors la duree du trajet (en minutes).
3. Calculer la longueur exacte et la duree exacte du trajet si C(6,0).
4, Parmi ces trois trajets, Iequel est le plus court (en distance).
Lequel est Ie plus rapide? Commenter les resultats.

Partie B : Recherche experimentale du minimum
On note x l'abscisse du point C. On a donc C(x; 0).

Demontrer que AC : √(×^2+25), et que CB=12-x
2.On designe par T la fonction exprimant la duree total du trajet en fonction de x.
a. Donner l'ensemble de definitions de T.
b. Demontrer que T(x) = 3√(x^2+25)+24-2x.

Mes reponses :
A) 1) grace a la forume √((x2-x1)^2+(y2-y1)^2), j'ai trouve que AC = 5 hm et CB= 12 hm
En utilisant la forumle du temps : T=d/v, j'ai trouve que pour aller de A a C elle a eu besoin de 15 min
et pour aller de C a B 24
Donc total = 39 min
2) je n'ai pas compris la question
3) Je ne l'ai pas compris non plus
4) depand de 2 et 3

B) 1)
j'ai reutilise la formule √((x2-x1)^2+(y2-y1)^2) pour les deux
2) je ne l'ai pas compris

Merci d'avance pour m'aider et desole pour les accents car j'utilise un clavier anglais donc veuillez m'excuser ;D

Bonjour Prince-Of-Darkness,

Il manque la figure.

Partie A.

Juste.
Calcule la distance AB (Pythagore) puis la durée du parcours en bateau.
Calcule la distance AC, puis le temps pour aller de A à C en bateau et de C à B à pied.
Compare les temps pour les trois trajets.

Partie B.
Même démarche que la partie A.
Le temps t = 3 AC + 2 CB.

Indique tes éléments de réponse et résultats si tu souhaites une correction.

oui desole

@Noemi Pour 2 de partie A, je ne pense pas que je peux utiliser le theoreme de Pythagore car ce n'est pas un triangle rectangle donc je vais utiliser la formule √((x2-x1)^2+(y2-y1)^2) . Qu'en pensez-vous ?

@Noemi 2)J'ai fait les calcules et j'ai trouve que la distance AB=13 hm et la duree = 39 min
3) j'ai trouve que :
Distance AC= √(61) hm
Temps AC= 3√(61)
Disance CB=6 hm
Temps CB= 12

La longueur exacte du trajet est donc = 6+√(61)
et La duree exacte du trajet = 12+3√(61)

Je ne sais pas comment je vais comparer le temps si C(6;0)

@Prince-Of-Darkness

Tu compares les trois temps
Cas 1 : durée 39 minutes
Cas 2 : durée 39 minutes
cas 3 : durée $12+36112+3\sqrt{61}$ = 35,43.. minutes

Compare ces trois durées.

@Noemi expliquez plus pour la question 2 de b SVP

@Prince-Of-Darkness

Pour le b) de la partie B,
Il faut calculer l'expression de la durée totale du parcours :
$\dfrac{AC}{v_1} + \dfrac{CB}{v_2}$
soit
$T (x) = 3 A C + 2 C B$

@Noemi Merci pour votre aide ;D

@Prince-Of-Darkness

Tu as terminé l'exercice ?

@Noemi Oui, j''ai termine l'exercice

@Prince-Of-Darkness

C'est parfait.