Maximum d'une fonction

BONSOIR, est-ce-que quelqu'un pourra m'aider svp voici le sujet:
Pour la proposition suivante, dites si elle est vraie ou fausse puis justifier votre réponse

On donne la courbe de la fonction f, définie sur R ,par: $f(x)=x2+2x+34x2+1f(x)=\dfrac{x^2+2x+3}{4x^2+1}$
f admet un maximum en x=0
merci à tous ceux qui vont m'aider.

Formule re-écrite en Latex par la modération.

Bonsoir ariel,

L'expression de la fonction est-elle : $f(x)=x2+2x+34x2+1f(x)=\dfrac{x^2+2x+3}{4x^2+1}$ ?

oui , au fait je doit prouver que c'est vrai ou faux et justifier ma réponse

@ariel

La réponse est faux et pour le démontrer, il faut calculer la dérivée et rechercher les variations de la fonction.

comment savoir que c'est faux ou vrai

La dérivée $\dfrac{-2(4x^2+11x-1)}{(4x^2+1)^2}$
La résolution de $f^{'} (x) = 0$ donne deux solutions mais aucune égale à 0.
Tu peux indiquer les variations de la fonction puis conclure que
$x = 0$ ne peux pas être un maximum

@ariel , bonjour (et bonjour @Noemi )

Une autre version possible plus rapide, si tu le souhaites.

@ariel, si la courbe t'est donnée (comme ça semble être le cas) ou si tu l'a réalisée, tu as dû trouver celle-ci.

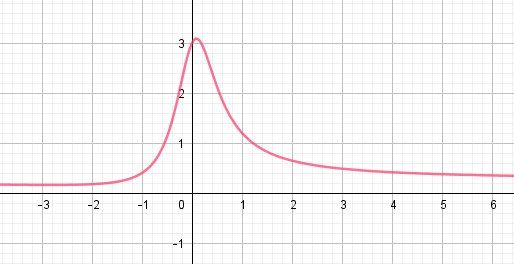
A y regarder de très près, le maximum n'est pas exactement pour x=0, mais pour une valeur très légèrement supérieure.

Si tu veux prouver que f n'admet pas de maximum pour x =0, sans étudier la fonction (dérivée et valeurs qui annulent la dérivée) :

Tu calcules f0) et tu trouves $f (0) = 3$

Tu calcules par exemple f(0.1)
$f(0.1)=0.12+2(0.1)+34(0.1)2+1=3.211.04=321104f(0.1)=\dfrac{0.1^2+2(0.1)+3}{4(0.1)^2+1}=\dfrac{3.21}{1.04}=\dfrac{321}{104}$
$f (0.1) = 3.08654 . . .$

$\gt f(0)$

Donc le maximum n'est pas atteint pour x=0.

Tu as le choix pour la méthode !

oui merci

De rien !

@ariel , je te donne une indication qui peut-t-être utile dans d'autres exercices à propos des propositions vraies ou fausses.

Pour prouver que la proposition indiquée dans ton énoncé était vraie, il aurait fallu prouver que :
Pour tout x de R, $\le f(0)$
L'étude générale des variations de la fonction aurait été indispensable.

Pour prouver que la proposition indiquée dans ton énoncé est fausse, un exemple (que l'on appelle contre exemple) suffit :
Il existe une valeur x de R telle que $\gt f(0)$

Bien sûr, le graphique était là pour aider à trouver une valeur de x telle que $\gt f(0)$
Sans la graphique pour aider (ou tableur ou autre) tu aurais été obligé de faire l'étude générale...et tu aurais trouvé que le maximum de f était pour $x=137−118x=\dfrac{\sqrt{137}-11}{8}$ qui est une valeur différente de 0 (plus précisément très légèrement supérieure à 0 ; à la calculette $0.088087 . . .$ )