Fonctions et intervalles

Bonjour, dans l'exercice nous avons une courbe représentative de f(x). Je vous joins le sujet. La question n 8 de l'exo 1 nous demande comment varie f(x) (l'intervalle) en fonction de x compris sur l'intervalle [-4;6]
Pouvez-vous m'expliquer la démarche svp? Merci d'avance

Bonjour Lisa59Maths,

Tu analyses le graphe pour $x$ variant dans l'intervalle $[- 4; 6]$ .
La fonction est-elle croissante, décroissante ?

Peux-tu transmettre le graphe ou l'équation de la fonction ?
Tu utilises l'icône image.

Bonjour,

Une illustration possible (en attendant que Lisa59Math donne la représentation graphique souhaitée).

Idée : f étant une fonction continue sur [-4,6], l'ensemble des images de x par f pour $x∈[−4,6]x\in [-4,6]$ est l'intervalle [m,M] , m étant la valeur minimale de f(x) et M la valeur maximale de f(x)

Dans l'exemple donnée, pour $x∈[−4,6]x\in[-4,6]$ , f est répresentée par la portion de courbe rouge.
La valeur minimale de f(x) est -20, obtenue pour x=2, donc m=-20
La valeur maximale de f(x) est 128, obtenue pour x=6, donc M=128

l'ensemble des images de x par f pour $x∈[−4,6]x\in [-4,6]$ est l'intervalle [-20,128]

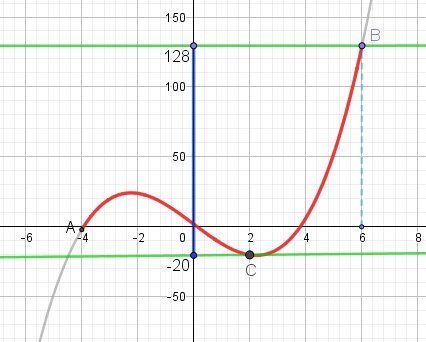
Pour tout x de [-4,6], on obtient un point N d'abscisse x (sur la portion de courbe rouge) , qui a une ordonnée y=f(x) comprise entre -20 et +128.