Exercice de math sur les équations

Bonjours à tous je vous demandes votre aide pour un dm en math sur un exercice que je n'ai pas très bien compris :
Une agence de location de voiture propose deux formules :
1er formule: forfait de 38euros et 0,12 euros le km
2em formule: 0,22 euros le km

1 : quelle est le prix payé pour 250 km avec la 1er formule ?
avec la 2 em formule ?
quelle est la formule la plus avantageuse ?

2: Meme question pour 500 km

3: a partir de combien de km la 1er formule est elle la plus rentable ?
on posera x , le nombre de km parcourus
J’espère que vous parviendrais a résoudre ce problème merci

Bonsoir Brik2lait,

Si on pose $x$ le nombre de kilomètres parcourues
Première formule le prix $P1(x)=0,12×x+38P_1(x) = 0,12 \times x + 38$
Deuxième formule, le prix $P2(x)=0,22×xP_2(x)=0,22\times x$

Bonjour,

@Brik2lait a dû terminer son exercice depuis plusieurs jours.

Quelques détails pour consultation éventuelle.

Les questions 1) et 2) sont des calculs numériques , la généralisation étant faite à la question 3) comme l'a indiquée @Noemi

1)Pour 250 km parcourus, avec la première formule , le prix est
$P1(250)=0.12×250+38=68P_1(250)=0.12\times250+38=68$

Pour 250 km parcourus, avec la seconde formule , le prix est
$P2(250)=0.22×500=55P_2(250)=0.22\times500=55$

On tire la conclusion sur la formule la plus avantageuse , c'est à dire prix le plus bas

2)**Pour 500 km parcourus **, avec la première formule , le prix est
$P1(500)=0.12×500+38=98P_1(500)=0.12\times500+38=98$

Pour 500 km parcourus, avec la seconde formule , le prix est
$P2(250)=0.22×500=110P_2(250)=0.22\times500=110$

On tire la conclusion sur la formule la plus avantageuse , c'est à dire prix le plus bas

3)Comme l'a indiqué @Noemi , x étant le nombre de km parcourus, pour $x≥0\boxed{x \ge 0}$ ,

Pour x km parcourus, avec la première formule , le prix est
$P1(500)=0.12x+38\boxed{P_1(500)=0.12 x+38}$

Pour x km parcourus, avec la seconde formule , le prix est
$P2(x)=0.22x\boxed{P_2(x)=0.22x}$

On doit résoudre : $P1(x)<P2(x)\boxed{P_1(x) \lt P_2(x)}$

$\lt 0.22x$ <=> $−0.10x<−38-0.10x\lt -38$ <=> $\gt 38$
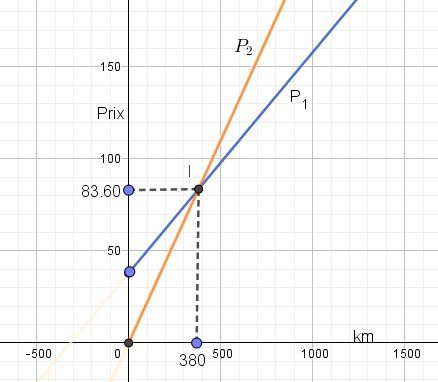
Au final : $x>380\boxed{x\gt 380}$

Représentation graphique pour illustration

Pour $x>380x\gt 380$ , la représentation graphique de $P_1$ est en dessous de la représentation graphique de $P_2$