Résolution d'une équation de la forme cos(a)=cos(b) et merci

[Aida Omrane]

Bonjour,
résoudre dans IR puis dans [0,2pi[ ,[-pi, pi] et ]-2pi, 3pi] l'équation cosx=cos3x

[Noemi]

Bonjour Aida-Omrane, (tu es en 5éme ?)

Tu appliques le cours :
$cosa=cosb$ équivalent à
$a=b+2k\pi$
$a=-b+2k\pi$ avec $k\in \mathbb{Z}$.

Indique tes solutions si tu souhaites une correction.

[mtschoon]

@Aida-Omrane , bonjour,

Ta question a été déplacée en 1S par la modération car la mettre en 6eme/5eme comme tu l'as fait n'a pas de sens ici.

[mtschoon]

Bonjour,
@Aida-Omrane a dû terminer son exercice depuis plusieurs jours.

Synthèse des résultats, pour consultation éventuelle.
Pour $k\in Z$
1er cas : $x=3x+2k\pi$ <=> $x=-k\pi$
Le plus simple est d'écrire $\boxed{x=k\pi }$ , c'est à dire $\boxed{x=0[\pi ]}$
Sur le cercle trigonométrique, les images ponctuelles correspondantes sont les points A et C
2ème cas ; $x=-3x+2k\pi$ <=> $x=\frac{2k\pi }{4}$
Le plus simple est d'écrire $\boxed{x=\frac{k\pi }{2}}$, c'est à dire $\boxed{x=0\left[\frac{\pi }{2}\right]}$
Sur le cercle trigonométrique, les images ponctuelles correspondantes sont les points A, B, C, D

Les valeurs obtenues au 1er cas faisant partie des valeurs obtenues au second cas, les solutions sont $\boxed{x=\frac{k\pi }{2}}$, c'est à dire $\boxed{x=0\left[\frac{\pi }{2}\right]}$

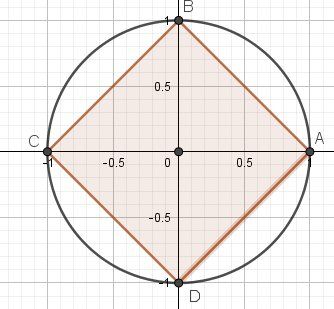
Conséquences :
Pour $x\in [0,2\pi [$ , les solutions sont $\boxed{0,\frac{\pi }{2},\pi ,\frac{3\pi }{2}}$ obtenues en donnant à k les valeurs 0,1,2,3
Pour $x\in [-\pi ,\pi [$ , les solutions sont $\boxed{-\pi ,-\frac{\pi }{2},0,\frac{\pi }{2}}$ obtenues en donnant à k les valeurs-2,-1,0,1
Pour $x\in ]-2\pi ,3\pi ]$, les solutions sont $\boxed{-\frac{3\pi }{2},-\pi ,-\frac{\pi }{2},\pi ,0,\frac{\pi }{2},\pi ,\frac{3\pi }{2},2\pi ,\frac{5\pi }{2},3\pi }$ obtenues en donnant à k les valeurs -3,-,2,-1,0,1,2,3,4,5,6.

[Black-Jack]

@mtschoon a dit dans Résolution de'une équation de la forme cos(a)=cos(b) et merci :

@Aida-Omrane , bonjour,

Ta question a été déplacée en 1S par la modération car la mettre en 6eme/5eme comme tu l'as fait n'a pas de sens.

Bonjour,

Cela n'a pas de sens ... sauf si Aida-Omrane est scolarisée dans un pays où on compte à l'endroit et pas à l'envers ...

Par exemple, en Belgique (et dans la plupart des autres pays hors France) la 1 S de France correspond à une 5ème.

[mtschoon]

Bonjour,
Vu que MathforU est un site français, il est heureux que les élèves français (ou pour lesquels l'enseignement correspond à l'enseignement français) qui viennent consulter , puissent s'y retrouver...c'est notre but.

Je suppose qu'en Belgique ou dans d'autres pays hors de France, il y a des forums d'aide mathématique que les élèves concernés peuvent consulter et qui correspondent exactement à leur scolarité.

Bien sûr, nous sommes très contents d'accueillir des élèves belges ou autres, (et c'est tant mieux si notre bonne réputation dépasse les frontières...), mais pour la nomenclature des niveaux, ce sont eux qui doivent s'adapter.