4. exercice vecteurs et produit scalaire

exercice vecteurs et produit scalaire

  • N

    On considère les points A(7;−2A(7;-2A(7;−2),B(−1;4)B(-1;4)B(−1;4), et C(−3;−2)C(-3;-2)C(−3;−2) dans un repère orthonormé. Le point A' est le milieu du segment [BC][BC][BC] et HHH est le projeté orthogonal de A′A'A′ sur le coté [AC][AC][AC].

    1. Faire une figure.
    2. Montrer que le triangle ABC est isocèle en A .
    3. Déterminer les coordonnées de A' et calculer le produit scalaire AA′→.AC→\overrightarrow{AA' }.\overrightarrow{AC} AA′.AC
    4. En déduire la longueur AHAHAH.
    5. Vérifier que les coordonnée de HHH sont (−2;−2)(-2;-2)(−2;−2).
    6. On appel I le milieu de segment [A′H][A'H][A′H]. Démontrer que (AI)(AI)(AI) et (BH)(BH)(BH) sont perpendiculaires.
  • mtschoon

    @nisrine , bonsoir,

    Ici, convivialité et politesse sont indispensables.
    Pense-y une autre fois si tu veux de l'aide.

    Pistes pour démarrer,

    1. Je te joins un schéma
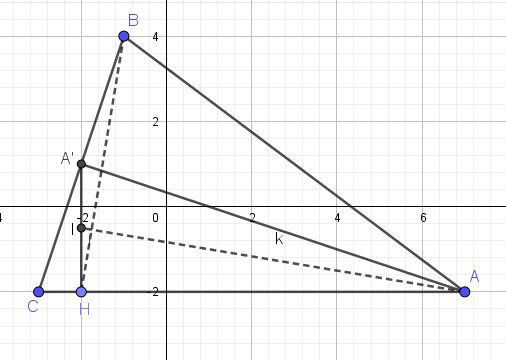
      Scalaire.jpg

    2. Regarde les formules de ton cours,
      AB=(xB−xA)2+(yB−yA)2AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}AB=(xB​−xA​)2+(yB​−yA​)2​
      AC=(xC−xA)2+(yC−yA)2AC=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}AC=(xC​−xA​)2+(yC​−yA​)2​

    Tu comptes et tu dois trouver AB=AC=10AB=AC=10AB=AC=10

    Essaie de poursuivre.
    Indique ce que tu as trouvé si tu as besoin d'aide et/ou vérification pour la suite.

  • N

    merci!! j'ai bien trouver cette valeurs et mon schéma correspond au votre. pour les coordonnées de A′A'A′ j'ai trouvé à l'aide d'un système (−2;1)(-2;1)(−2;1) ensuite pour le produit scalaire je trouve 909090 et là je suis coincé à la question 4...

  • mtschoon

    c'est bon pour tes réponses à la 3)

    Piste pour la 4)

    H étant le projeté de A' sur (AC)

    AA′→.AC→=AH→.AC→\overrightarrow{AA'}.\overrightarrow{AC}=\overrightarrow{AH}.\overrightarrow{AC}AA′.AC=AH.AC

    Donc AH→.AC→=90\overrightarrow{AH}.\overrightarrow{AC}=90AH.AC=90

    Tu peux en déduire AH

  • N

    d'accord mercii beaucoup du coup comme [AC]=10cm[AC]=10 cm[AC]=10cm donc pour que sa fasse 909090 il faut multiplié par 9 donc AH=9cmAH=9cmAH=9cm

  • N

    pour vérifier les coordonnées de HHH j'ai utilisé la formule suivante:
    vec(A′H).vec(HA)=x(A′H)x(HA)+y(A′H)y(HA)vec(A'H).vec(HA)=x(A'H)x(HA)+y(A'H)y(HA)vec(A′H).vec(HA)=x(A′H)x(HA)+y(A′H)y(HA) en remplaçant avec les valeurs et comme je trouve un résultat de donc les coordonnées de H sont bien (−2;−2)(-2;-2)(−2;−2)

  • mtschoon

    Ta démarche est bonne pour la 4) et 5)
    Pour la 4), il faut bien détailler. J'espère que c'est ce que tu as fait.
    AH→.AC→=AH×AC×cos(AH→,AC→)\overrightarrow{AH}.\overrightarrow{AC}=AH\times AC \times cos(\overrightarrow{AH},\overrightarrow{AC})AH.AC=AH×AC×cos(AH,AC)
    AH→.AC→=AH×AC×cos(0)=AH×AC×1=AH×AC=90\overrightarrow{AH}.\overrightarrow{AC}=AH\times AC \times cos(0)=AH\times AC\times 1=AH\times AC=90AH.AC=AH×AC×cos(0)=AH×AC×1=AH×AC=90
    D'où les calculs faits.

    Pour la 6), tu ne dois pas avoir de difficultés

    Tu calcules les coordonnées de I

    Tu calcules AI→.BH→\overrightarrow{AI}.\overrightarrow{BH}AI.BH et tu dois trouver
    AI→.BH→=0\overrightarrow{AI}.\overrightarrow{BH}=0AI.BH=0

    Tu tires la conclusion.

    Bon travail.

  • C

    Bonjour @mtschoon, je voudrais savoir quels sont les calculs pour trouver les coordonnées de H à la question 4 car j'ai essayé pleins de calculs et je ne trouve pas les coordonnées (-2;-2). Pouvez-vous aussi me dire les calculs pour démonter que (AI) et (BH) sont perpendiculaires?

    Je n'y arrive pas
    Merci beaucoup d'avance,

  • mtschoon

    @clara-mra , bonjour,

    J'espère que tu connais les propriétés du produit scalaire.
    D'où AH×AC=90AH\times AC=90AH×AC=90 <=> AH×10=90AH\times 10=90AH×10=90 <=> AH=9AH=9AH=9

    Piste pour la suite,

    Le vecteurAH→\overrightarrow{AH}AH a donc pour coordonnées (−9,0)(-9,0)(−9,0)

    D'où :
    xH−xA=−9x_H-x_A=-9xH​−xA​=−9 <=> xH−7=−9x_H-7=-9xH​−7=−9 tu termines
    yH−yA=0y_H-y_A=0yH​−yA​=0 <=> yH+2=0y_H+2=0yH​+2=0 tu termines

    Pour démontre que (AI) et (BH) sont orthogonales :

    Tu commences par calculer les coordonnées de I , milieu de [A'H]
    Ensuite, tu calcules les coodonnées (X,Y)(X,Y)(X,Y) de AI→\overrightarrow{AI}AI ainsi que les coordonnées (X′,Y′)(X',Y')(X′,Y′) de BH→\overrightarrow{BH}BH

    AI→.BH→=XX′+YY′\overrightarrow{AI}.\overrightarrow{BH}=XX'+YY'AI.BH=XX′+YY′

    Tu dois trouver ainsi AI→.BH→=0\overrightarrow{AI}.\overrightarrow{BH}=0AI.BH=0, d'où la conclusion.

    Bons calculs.

    Reposte si tu n'aboutis pas.

    L 2 réponses
  • L

    @mtschoon

  • L

    @mtschoon
    Bonjour, je suis à la dernière question j’ai donc calculer les coordonnées de I puis le produit scalaire AI•BH mais je ne trouve pas 0 . Pouvez vous donc me donner vos calculs pour que je compare car je l’ai refait plusieurs fois et je tombe toujours sur le même résultat j’aimera donc voir où est mon erreur .
    Cordialement

  • mtschoon

    @line8572 , bonsoir,

    Ce serait bien que tu donnes ce que tu as trouvé, au moins les coordonnées de III, pour comprendre où est ton erreur, vu que la marche à suivre est indiquée juste au dessus dans la réponde donnée @clara-mra

  • mtschoon

    @line8572 , bonjour,

    Pour que tu puisses revoir tes calculs, je te donne les coordonnées de tous les points nécessaires.

    H(−2,−2)H(-2,-2)H(−2,−2)
    A(7,−2)A(7,-2)A(7,−2)
    B(−1,4)B(-1,4)B(−1,4)
    C(−3,−2)C(-3,-2)C(−3,−2)
    A′A'A′ milieu de [BC][BC][BC] : (−1−32,4−22)=(−2,1)(\dfrac{-1-3}{2}, \dfrac{4-2}{2})=(-2,1)(2−1−3​,24−2​)=(−2,1)
    III milieu de [A′H][A'H][A′H] : (−2−22,1−22)=(−2,−12)(\dfrac{-2-2}{2}, \dfrac{1-2}{2})=(-2,\dfrac{-1}{2})(2−2−2​,21−2​)=(−2,2−1​)

    Avec ça, tu ne dois pas avoir de difficultés pour calculer les coordonnées de AI→\overrightarrow{AI}AI et BH→\overrightarrow{BH}BH et le produit scalaire AI→.BH→\overrightarrow{AI}.\overrightarrow{BH}AI.BH qui doit faire 000

    Donne tes calculs si tu n'y arrives pas, pour obtenir une vérification.

    Bons calculs .

Se connecter pour répondre