Angle molécule méthane - centre d'un tétraèdre régulier.

bonjour
voici l'énoncé
déterminer la mesure de l'angle formé par deux liaisons C-H , en degré (molécule de méthane)
données :
C est le centre du tétraèdre régulier EFGH
I milieu de [EF]
J milieu de [HG]
$ECF^=FCG^=GCH^=HCE^\widehat{ECF}=\widehat{FCG}=\widehat{GCH}=\widehat{HCE}$

comment déterminer l'angle alors que je n'ai aucune mesure ?? merci !!

(angles re-écrits en Latex par la modération)

Bonjour sixxtinn,

Tu dois déterminer l'angle formé par le centre d'un tétraèdre régulier et deux sommets de ce tétraèdre.

Calcule la dimension d'une hauteur pour le triangle équilatéral de la base du tétraèdre.
Calcule ensuite la mesure du segment reliant un sommet de la base avec le pied de la hauteur du tétraèdre.
Calcule la hauteur du tétraèdre en fonction de l'arête puis l'angle formé par cette hauteur avec une arête.
Tu en déduis ensuite la mesure de l'angle recherchée.

je penseque h=a.racine de 3/2

@sixxtinn

Oui

La dimension d'une hauteur pour le triangle équilatéral de la base du tétraèdre est $a\dfrac{\sqrt3}{2}$ .
Si on prend pour base le triangle $F G H$ et que l'on note $H_1$ le pied de la hauteur du tétraèdre issu du sommet $E$
Soit $FH_1$ la mesure du segment reliant un sommet de la base avec le pied de la hauteur du tétraèdre. Tu utilises le fait que le centre de gravité est au 2/3 de la hauteur, soit $FH1=a33FH_1 = a\dfrac{\sqrt3}{3}$ .

Calcule la hauteur du tétraèdre en fonction de l'arête (Tu peux utiliser la relation de Pythagore) puis tu calcules l'angle formé par cette hauteur avec une arête.
Tu en déduis ensuite la mesure de l'angle recherchée.

le pied de la hauteur correspond à C centre du tétraèdre ?

@sixxtinn

Non, le pied de la hauteur se situe au centre de gravité du triangle qui constitue la base du tétraèdre.
Pour calculer la hauteur tu utilises le triangle rectangle constitué de la hauteur du tétraèdre, une arête et le segment $FH_1$ .
Donc la hauteur $h$ , se calcule par $h^2 + FH_1^2 = a^2$ ou $EH_1^2 + FH_1^2 = EF^2$
soit $EH12=h2=a2−(a33)2=23a2EH_1^2 = h^2 = a^2 - (a\dfrac{\sqrt3}{3})^2 = \dfrac{2}{3}a^2$

Je te laisse poursuivre en utilisant la trigonométrie dans le triangle $FEH_1$ ; $c o s F E C = . . .$

désolée, en fait je pense qu'il faut utiliser les produits scalaires car c'est dans cette leçon

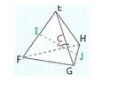
donc il faut peut-être commencer par dire dans IJG rectangle en J (donc 90°) ...???

@sixxtinn

Oui, le produit scalaire est une autre solution. Tu aurais du le signaler dans le titre, j'ai cru que c'était en lien avec le cours de chimie.

désolée !!!

@sixxtinn et @Noemi , bonjour,

@sixxtinn ,
Si tu veux une version vectorielle avec le produit scalaire, je me permets une proposition, mais tout dépend de ton cours...et je ne suis pas sûre qu'elle convienne...elle est très courte, mais demande peut-être des notions que tu ne connais pas...
Je la propose tout de même, vu sa simplicité.

C est le centre du tétraèdre régulier , c'est à dire l'isobarycentre des points E,F,G,H

$CE→+CF→+CG→+CH→=0→\overrightarrow{CE}+\overrightarrow{CF}+\overrightarrow{CG}+\overrightarrow{CH}=\overrightarrow{0}$

En faisant le produit scalaire avec $CE→\overrightarrow{CE}$

$CE→.(CE→+CF→+CG→+CH→)=0\overrightarrow{CE}.(\overrightarrow{CE}+\overrightarrow{CF}+\overrightarrow{CG}+\overrightarrow{CH})=0$

On développe et on simplifie car on trouve trois produits scalaires égaux et on obtient :
$CE→.CE→+3CE→.CF→=0\overrightarrow{CE}.\overrightarrow{CE}+3\overrightarrow{CE}.\overrightarrow{CF}=0$

En appelant a la distance de C aux points E,F,G,H , et $θ\theta$ l'angle cherché, l'égalité précédente devient

$a2+3(a×a×cosθ)=0a^2+3(a\times a\times cos\theta)=0$

Après transformation, vu que $a≠0a\ne 0$ , on trouve

$cosθ=−13cos\theta=-\dfrac{1}{3}$

On cherche une valeur approchée de $θ\theta$ à la calculette

Ceci n'est qu'une proposition, avec très peu de calculs... Voir si elle convient, ce qui n'est pas sûr.

A mon avis, il faut utiliser le milieu du segment,
donc calculer le produit scalaire $FG→.FJ→\overrightarrow{FG}.\overrightarrow{FJ}$ .
puis le produit scalaire $EF→.EH1→\overrightarrow{EF}.\overrightarrow{EH_1}$ .

et oui la 1ére méthode me parait compliquée car je n’ai pas vu ces notions en cours
je pense aussi que la 2eme calculer le produit scalaire est la bonne

@sixxtinn

L'énoncé indique le milieu de segment, donc j'opterais pour une autre méthode.
Calcul de $FG→.FJ→\overrightarrow{FG}.\overrightarrow{FJ}$ qui donne pour résultat : $\sqrt\dfrac{3}{2}a$
Tu en déduis la mesure de $FH_1$ avec $H_1$ le pied de la hauteur du tétraèdre.
Puis tu calcules la mesure de la hauteur $EH_1$ et tu utilises le calcul du produit scalaire
$EF→.EH1→\overrightarrow{EF}.\overrightarrow{EH_1}$ avec les deux relations pour en déduire la valeur du cosinus, puis de l'angle.

@Noemi , Tout à fait d'accord, mais quelle lourdeur ! ! !

@sixxtinn , la proposition que je t'ai faite utilise les propriétés du produit scalaire, mais elle nécessite que tu connaisses aussi la notion d'isobarycentre. Tu peux essayer de la comprendre.

Si tu ne connais pas la définition d'isobaycentre, tant pis, tu verras cela plus tard, passe par les points I et J et démarre comme te l'indique Noemi.
C'est beaucoup plus "lourd", mais tu n'as peut-être pas le choix...

Quelle que soit la méthode, tu devrais aboutir à
$cosθ=−13cos\theta=-\dfrac{1}{3}$

merci de votre aide