Devoir maison de mathématiques : Aire et inéquation
-
Ggregory dernière édition par mtschoon
Bonjour, j'ai un devoir maison de mathématiques à faire pour demain et je bloque sur deux exercices, voici le premier:
ABCD est un rectangle tel que AB = 6 et AD = 4. On note M, N, P, Q les points appartenant respectivement aux segments [AB], [BC], [CD] et [DA] tels que AM = BN = CP = DQ. Déterminer les postitions du point M pour lesquelles l'aire du quadrilatère M N P Q est au moins égale à la moitié de l'aire du rectangle ABCD.- Faire une figure ( c'est bon)
- On pose AM= x. Exprimer l'aire de M N P Q en fonction de x.
- Traduire le problème par une inéquation, la résoudre et conclure.
Merci d'avance pour le temps que vous me consacrerez.
-
Bonjour leo04,
Question 2,
Exprime l'aire des triangles rectangles en fonction de xxx.
Exemple l'aire du triangle rectangle MBN = (6−x)x2\dfrac{(6-x)x}{2}2(6−x)x
Puis tu calcules l'aire du rectangle à laquelle tu soustrais l'aire des 4 triangles rectangles.Indique tes éléments de réponse si tu souhaites une correction
-
mtschoon dernière édition par mtschoon

Bonjour,
Pour éclairer l'explication si besoin.
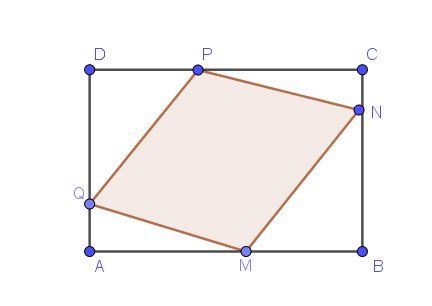
-
mtschoon dernière édition par mtschoon

Bonjour,
Apparemment, @leo04 a terminé son exercice.
Quelques pistes pour consultation éventuelle,
AM=BN=CP=DQ=x
MB=DP=6-x
NC=QA=4-xPour que la construction soit possible, nécessairement , x doit satisfaire à la condition x∈[0,4]\boxed{x\in [0,4]}x∈[0,4]
En prenant la formule de l'aire d'un triangle rectangle,
aire(AMQ)=aire(NCP)=x(6−x)2aire(AMQ)=aire(NCP)=\dfrac{x(6-x)}{2}aire(AMQ)=aire(NCP)=2x(6−x)
aire(MBN)=aire(DQP)=x(4−x)2aire(MBN)=aire(DQP)=\dfrac{x(4-x)}{2}aire(MBN)=aire(DQP)=2x(4−x)
La somme S des aires de ces 4 triangles vaut :
S=x(6−x)+x(4−x)=−2x2+10xS=x(6-x)+x(4-x)=-2x^2+10xS=x(6−x)+x(4−x)=−2x2+10xaire(ABCD)=6×4=24aire (ABCD)=6\times 4=24aire(ABCD)=6×4=24
donc,
aire(MNPQ)=24−(−2x2+10x)=2x2−10x+24aire(MNPQ)=24-(-2x^2+10x)=\boxed{2x^2-10x+24}aire(MNPQ)=24−(−2x2+10x)=2x2−10x+24aire(MNPQ)≥12aire(ABCD)aire(MNPQ)\ge \dfrac{1}{2}aire(ABCD)aire(MNPQ)≥21aire(ABCD) équivaut à :
2x2−10x+24≥122x^2-10x+24\ge 122x2−10x+24≥12 <=> 2x2−10x+12≥02x^2-10x+12\ge 02x2−10x+12≥0 que l'on peut réduire à
x2−5x+6≥0\boxed{x^2-5x+6\ge 0}x2−5x+6≥0
Inéquation du second degré à résoudre à résoudre sur R puis restreindre à [0,4]Après calculs , x∈[0,2]∪[3,4]\boxed{x\in [0,2] \cup [3,4]}x∈[0,2]∪[3,4]
-
Ggregory dernière édition par
Bonjour, gros problème d'ordinateur + maladie depuis, je ne l'avais pas finie et dois le rendre à la rentrée. Je m'y remets immédiatement...
-
Ggregory dernière édition par
Pour la question 2, je trouve que l'air de MBN+QDF = 6x-x2 et que celle de QAM+ NCP = 4x-x2 donc l'aire de MNPQ = 24 -10x -2x**2. Est-ce cela ?
-
Ggregory dernière édition par
Non pardon, 24 -10x + 2x**2
-
Ggregory dernière édition par
Je n'avais pas regarder votre message... c'est donc bon. Cependant après plusoeurs relectures je ne comprends toujours pas comment faire la question 3. Merci de votre aide
-
mtschoon dernière édition par mtschoon

@leo04 , bonjour,
Oui, aire(MNPQ)=2x2−10x+24aire(MNPQ)=2x^2-10x+24aire(MNPQ)=2x2−10x+24
C'est bien ce que tu as trouvé.Pour l'inéquation relative à la question 3), j'ai indiqué des pistes (relis ma réponse)
Je détaille un peu si besoin.
aire(ABCD)=AB×AD=6×4=24aire(ABCD)=AB\times AD=6\times 4=24aire(ABCD)=AB×AD=6×4=24
L'énoncé indique :
"l'aire du quadrilatère M N P Q est au moins égale à la moitié de l'aire du rectangle ABCD"Cela se traduit par l'inéquation:
2x2−10x+24≥12×242x^2-10x+24\ge\dfrac{1}{2}\times 242x2−10x+24≥21×24 c'est à dire :
2x2−10x+24≥122x^2-10x+24\ge 122x2−10x+24≥12 c'est à dire
2x2−10x+24−12≥02x^2-10x+24-12\ge 02x2−10x+24−12≥0 c'est à dire
2x2−10x+12≥02x^2-10x+12\ge 02x2−10x+12≥0En divisant chaque membre par 2 (pour simplifier les calculs), on obtient
x2−5x+6≥0\boxed{x^2-5x+6\ge 0}x2−5x+6≥0Regarde ton cours pour résoudre une inéquation du second degré et reposte si tu n'y arrives pas.
-
mtschoon dernière édition par mtschoon

@leo04 , je te mets les pistes pour résoudre l'inéquation.
Tu cherches d'abord les valeurs x1x_1x1 et x2x_2x2 qui annulent le polynôme x2−5x+6x^2-5x+6x2−5x+6, c'est à dire les solutions de l'équation x2−5x+6=0x^2-5x+6=0x2−5x+6=0
Tu dois trouver (voir les formules du cours)
Δ=1\Delta=1Δ=1
x1=2x_1=2x1=2
x2=3x_2=3x2=3
Ensuite, tu utilises le théorème relatif au signe d'un polynôme du second degré(signe de a, signe de(-a), signe de a) (voir cours) ici, a=1.

-
Ggregory dernière édition par
c'est parfait merci, mais je ne comprends pas la présence de 0 et 4 dans les x du tableaux.
-
mtschoon dernière édition par

@leo04 ,
Il faut penser aux conditions d'existence de x, liées à la construction du parallélogramme MNPQ
AM=BN=x donc nécessairement x≥0x\ge 0x≥0
M∈[AB]M \in [AB]M∈[AB] donc nécessairement, vu que AB=6, x≤6x\le 6x≤6
Mais, cela n'est pas suffisant pour terminer la construction du parallélogramme MNPQA partir de M, il faut placer N sur [BC] tel que BN=x
Vu que BC=4, nécessairement x≤4x \le 4x≤4Il n'y a pas de nouvelles contraintes pour placer P et Q
CONCLUSION : 0≤x≤4\boxed{0\le x\le 4}0≤x≤4
Etude de l'inéquation se fait donc sur l'intervalle [0,4]
-
Ggregory dernière édition par
ok merci beaucoup, a la fin les solutions sont donc [0;2]union[3;4] ?
-
mtschoon dernière édition par

@leo04 , c'est exact.
Tu as bien compris. C'est bien !