Devoir numéro 6- Aire d'un rectangle en fonction de x

ABC est un triangle rectangle en A tel que AB=5cm et AC=3cm.
Le point M est mobile sur le segment [AB].
On veut déterminer la position de M qui rend l’aire du rectangle AMNP maximale.

On note AM=x.
Quelles sont les valeurs possibles prises par x?
On note A(x) l’aire du rectangle AMNP. Montrer que A(x)= -3/5*x² + 3x
Développer et réduire l’expression
B= -3/5(x-5/2)²+5/14
En déduire que pour tout x appartient à l’intervalle [0;5] , A(x)⩽5/14
Répondre au problème.

Remarque de la modération :
Faute d'énoncé
@vavouille a confondu 5/14 avec $154\dfrac{15}{4}$

Bonsoir vavouille (Marque de politesse à ne pas oublier !!)

Indique tes éléments de réponse et la question qui te pose problème.

Comment sont placés les points N et P ?

$A M = x$ , or $A B = 5$ et le point M est mobile sur le segment $[A B]$ donc $x$ varie de ....
Applique la propriété de Thalès.

Vérifie l'énoncé.

Bonjour @Noemi et @vavouille ,

@vavouille , comme te l'a indiqué Noemi, ton énoncé est incomplet car on ne sait pas où sont N et P.

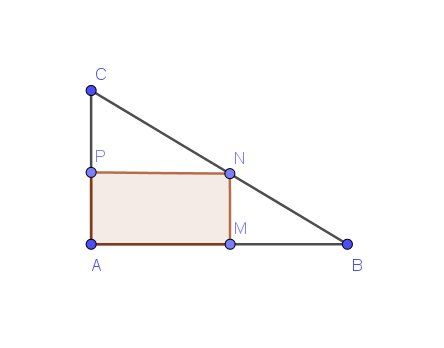
Je suppose que N est sur [BC] et P est sur [AC] de façon que AMNP soit un rectangle.
Je joins le schéma correspondant à cela.
Ce doit être correct car cette disposition correspond à l'expression de A(x) donnée dans l'énoncé.

Tiens nous au courant, si tu as besoin.

Bonjour,

Visiblement, @vavouille a déja fait son exercice (ou alors il l'a laissé...).

Quelques pistes pour consultation éventuelle, en complétant les indications de @Noemi

1)La distance AM varie de 0 à 5 donc $x∈[0,5]x\in [0,5]$

2) $A(x)=AM×APA(x)=AM\times AP$
$A M = x$ .
Il reste à calculer $A P = A C - C P = 3 - C P$

En utilisant le théorème de Thalès appliqué aux triangles CNP et CBA
$CPCA=NPBA\dfrac{CP}{CA}=\dfrac{NP}{BA}$ c'est à dire $CP3=x5\dfrac{CP}{3}=\dfrac{x}{5}$ c'est à dire $CP=3x5CP=\dfrac{3x}{5}$

Au final,
$AP=3−3x5=15−3x5AP=3-\dfrac{3x}{5}=\dfrac{15-3x}{5}$
Aire ( $A M N P$ )=A(x) = $x(15−3x5)=−3x25+3xx(\dfrac{15-3x}{5})=-\dfrac{3x^2}{5}+3x$

3)L'expression de B(x) écrite dans l'énoncé est fausse car @vavouille a confondu 5/14 avec 15/4

$B(x)=−35(x−52)2+154B(x)=-\dfrac{3}{5}\biggl(x-\dfrac{5}{2}\biggl)^2+\dfrac{15}{4}$
En développant et réduisant B(x), on trouve
$B (x) = A (x)$

Conclusion utile : $A(x)=−35(x−52)2+154\boxed{A(x)=-\dfrac{3}{5}\biggl(x-\dfrac{5}{2}\biggl)^2+\dfrac{15}{4}}$

Vu qu'un carré est nécessairement positif (au sens large) :
$(x−52)2≥0\biggl(x-\dfrac{5}{2}\biggl)^2 \ge 0$ donc $−35(x−52)2≤0-\dfrac{3}{5}\biggl(x-\dfrac{5}{2}\biggl)^2 \le 0$ donc
$\le \dfrac{15}{4}$

5)Conséquence : Le maximum de A(x) est $154\dfrac{15}{4}$
Il est atteint lorsque $(x−52)2=0\biggl(x-\dfrac{5}{2}\biggl)^2 =0$ c'est à dire $x=52x=\dfrac{5}{2}$
Le point M est alors au milieu de [AB]