Exercice Cylindre de SECONDE

Bonjour !
Je suis en Seconde et j'ai besoin d'un petit coup de pouce pour mon DM , en effet on me donne pour consigne :
Dans un récipient de rayon 10cm et de hauteur 30cm , on place une bille de rayon 4cm.
On verse de l'eau jusqu'à recouvrir exactement la bille.
On retire ensuite la bille et on la remplace par une autre bille de rayon R différent de 4cm.
Est-il possible que l'eau recouvre exactement la nouvelle bille ?

Merci d'avance !

Bonjour ornemaths,

Le volume, en $cm^3$ occupé par la bille et l'eau est : $\pi\times 10^2\times 8$
Calcule le volume de la bille, tu en déduis, le volume d'eau versée pour recouvrir entièrement la bille.
Tu écris ensuite une équation : Volume de la nouvelle bille + volume d'eau = volume d'un cylindre de hauteur le diamètre de la nouvelle bille.
Tu résous ensuite cette équation.

Indique tes éléments de réponse si tu souhaites une correction.

Volume de la bille : $\dfrac{4}{3} \pi R^3$ .
Si $4\ cm$ , $V = . . . .$
Tu peux laisser la valeur exacte avec $π\pi$ .

Ou en es-tu ornemaths ?

J'espère que tu as fait les calculs et que tu n'attends pas une réponse complète.

Calcul du Volume, en $cm^3$ occupé par la bille et l'eau : $times102×8=....V_t = \pi \ times 10^2 \times 8 = ....$
Calcul du volume de la bille : $Vb=43π×43=.....V_b= \dfrac{4}{3} \pi \times 4^3 = .....$
Calcul du volume d'eau versée : $V_e=V_t - V_b = ....$
Soit r le rayon cherché : Il faut résoudre l'équation $43π×r3+Ve=π×102×2r\dfrac{4}{3}\pi\times r^3 + V_e = \pi\times 10^2\times 2r$ .
Equation du troisième degré en $r$ donc trois solutions mais une est connue, c'est $r = 4$ .
On peut donc mettre $(r - 4)$ en facteur puis résoudre l'équation du second degré pour déterminer les deux valeurs possibles pour le rayon $r$ .

Bonjour !
Merci énormément pour vos réponses , ayant effectuer les calculs je ne trouve toujours pas la logique qui s'y coule :
Calcul du Volume, en cm3 = 800π
Calcul du volume de la bille = 268,08
Calcul du volume d'eau versée = 2513,27 - 268,08 = 2245,19
mais pour ce qui est de l'étape je ne comprend pas
Merci !!!

Bonjour

Comme cela t'a été judicieusement conseillé ... il FAUT laisser Pi en littéral dans les calculs.

V cyl = 800.Pi cm³ (OK)

V bille = 256/3 * Pi cm³ (ne pas calculer la valeur en décimal ...)

V eau = V cyl - V bille = (800 - 256/3)*Pi (cm³)

V eau = (2144/3) * Pi cm³ (ne pas calculer la valeur en décimal ...)

Comme indiqué dans le message précédent de Noemi :

4/3 Pi * r³ + V eau = Pi * 10^2 * 2r

donne : 4/3 Pi * r³ + (2144/3) * Pi = Pi * 10^2 * 2r

Et on peut simplifier par Pi (d'où l'intérêt d' avoir laisssé Pi en littéral)

4/3 * r³ + (2144/3) = 10^2 * 2r

Il te reste à trouver les solutions de cette équation ... en sachant qu'une de ces solutions est r = 4

...

Bonjour,

Cet énoncé (ou apparenté) figure sur de nombreux sites de maths (avec solutions) depuis 2012, mais dans des rubriques de Terminale ou Première.
S'il n' y a pas des aides dans l'énoncé, un élève de seconde n'a pas les techniques pour factoriser par (r-4) ni même résoudre seul une équation du second degré.
Il n'a pas le TVI non plus à sa disposition

Ici, l'énoncé indique :
"Est-il possible que l'eau recouvre exactement la nouvelle bille ?"
Je pense qu'il faut répondre dans l'esprit "SECONDE" comme le demande @ornemaths. sans chercher la valeur exacte $r=138−2r=\sqrt{138}-2$ .
Il faut seulement prouver que cela est possible.

En utilisant, par exemple, sa calculatrice (avec la fonction Table, r s'appelant x), @ornemaths peut faire un tableau de valeurs et en déduire une représentation graphique en reliant les points par un trait continu, puis tirer la conclusion.

Piste éventuelle,

En multipliant par $34\dfrac{3}{4}$ , l'équation peut se simplifier en
$r3−150r+536=0\boxed{r^3-150r+536=0}$

@ornemaths peut faire un tableau de valeurs pour $r∈[0,10]\boxed{r\in[0,10]}$ (vu le rayon du récipient) de la fonction f définie par $f(r)=r3−150r+536\boxed{f(r)=r^3-150r+536}$ .

Puis, avec les points obtenus avec le tableau de valeurs, il peut représenter graphiquement f pour $r∈[0,10]\boxed{r\in[0,10]}$

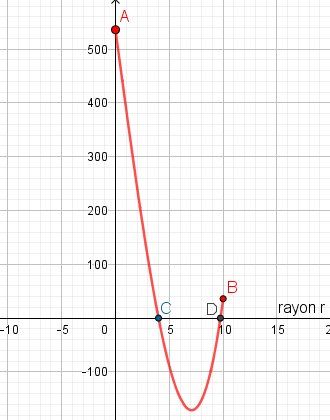
Points d'intersection de la représentation graphique de la fonction f en rouge (allant du point A d'abscisse 0 au point B d'abscisse 10) avec l'axe des abscisses :
C d'abscisse 4 et D d'abscisse voisine de 9.7

Enfin, il peut conclure.