Fonction logarithme avec limites

Bonjour, bonjour!
Pourriez-vous m'aider pour un dm?

On souhaite retrouver le résultat du cours par une autre méthode : lim(x tend vers + inf) ln(x)/x = 0

On nous demande d'étudier les variations de la fonction f définie sur [1;+infini[ par f(x)= ln(x) - (racine carré de x)
On nous demande de montrer que pour tout x E [1;+infini[, 0<ou= ln(x)/x <ou = 1/(racine carré de x). Déduire lim (x tend vers + inf) ln(x)/x
Soit n un entier naturel non nul
Démontrer que pour tout x E ]0; +inf[, e^x/x^n= e^x(1-n(ln(x)/x)). Déduire lim (x tend vers + inf) e^x/ x^n

Pour la 1), j'ai dérivée et j'ai trouvée que f'(x)= 1/x - 1/2(racine de x). Or 1/x supérieur à 0 et - 1/2(racine de x) <0. Donc elle est décroissante?

@Constance bonjour,

Piste pour démarrer,

Pour le 1), l dérivée donnée est bonne mais pour trouver son signe, commence pour réduire au même dénominateur $f′(x)=1x−x2x=22x−x2x=2−x2xf'(x)=\dfrac{1}{x}-\dfrac{\sqrt{x}}{2x}=\dfrac{2}{2x}-\dfrac{\sqrt{x}}{2x}=\dfrac{2-\sqrt x}{2x}$

Pour $x≥1x\ge 1$ , $2x>02x\gt 0$

Le signe de f'(x) est donc du signe du numérateur que tu étudies.

@mtschoon J'avais réduit au même déno mais je n'étais pas sur...
2- (racine de x) sur l'intervalle donné est donc strictement positif? La fonction f est donc croissante?

@Constance ,

Il faut étudier correctement le signe de $2−x2-\sqrt x$

$2−x=02-\sqrt x=0$ <=> $x=2\sqrt x =2$ <=> $x = 4$
$2−x>02-\sqrt x\gt 0$ <=> $x<2\sqrt x \lt 2$ <=> $x<4x\lt 4$
$2−x<02-\sqrt x\lt 0$ <=> ... (tu complètes)

@mtschoon Merci beaucoup!
Pour la question n°2 on doit utiliser le théorème des gendarmes?

@Constance

J'espère que tu as complété le signe de $2−x2-\sqrt x$ et qure tu as fait le tableau de variation de f.
Je t'indique ce que tu dois trouver

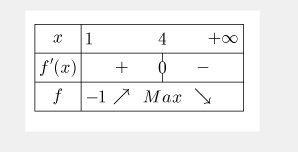
La valeur Max est f(4)=ln(4)-2 qui est strictement négative (tu peux prendre une valeur approchée à la calculette -0.6...)

Conséquence :

Pour tout $\ge 1$ , $f(x)≤0\boxed{f(x) \le 0}$
(j'aurais pu écrire $\lt 0$ mais il vaut mieux écrire l'inégalité au sens large en vue de la suite)

Avec cette conséquence, à la question 2, tu dois, comme tu l'indiques, utiliser le théorème des deux gendarmes.

@mtschoon Oui j'avais trouvée ça, merci beaucoup!

@Constance , c'est bien.

J'espère qu'avec le théorème des deux gendarmes tu as trouvé que :

$0≤lnxx≤1x0\le \dfrac{lnx}{x}\le \dfrac{1}{\sqrt x}$

d'où:

$lim⁡x→+∞lnxx=0\displaystyle \boxed{\lim_{x\to +\infty}\dfrac{lnx}{x}=0}$

Remarque :
Si tu as besoin d'aide sur la 3), il faudra re-écrire ce qu'il faut démontrer car l'égalité que tu donnes est peu lisible et bizarre...

@mtschoon Oui j'ai trouvée ça! Merci

De rien,@Constance ,