les fonctions généralités

bonjour vous pouvez m'aidez svp
abcd est un carré de coté 4
pour tout point m du segment [AB] on construit les carrés AMEF et CHEN on s'intéresse à l'aire hachurée on pose AM=x exprimer en fonction de x l'aire de la partie hachurée
on pose M=x

exprimer en fonction de x l'aire de la partie hachurée
quel est l'ensemble de definition de la fonction f , précedente
peut on placer M pour que l'aire de la partie hachurée soit égale à 11cm²

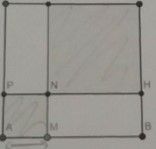
les points sont dans les ordres suivants
D H C
F E N
A M B

Bonsoir pouvens ,

Les points que tu indiques ne correspondent pas à la figure.
L'aire du petit carré est égale $x^2$ et
l'aire de l'autre carré est $4-x)^2$ .

Tu peux en déduire l'aire totale.

je mis les points car ça ne correspond pas à l'énoncé

du coup pour la 1
l'aire est 4

@pouvens

Non l'aire $A(x) = x^2+ (4-x)^2$
Développe cette expression et simplifie la.

@Noemi a dit dans les fonctions généralités :

x2+(4−x)2

x²+4x²-x²

@pouvens

$A(x) = x^2+ (4-x)^2 = x^2 + 16 - 8x+x^2 = 2x^2 -8x + 16$ .

a ok merci
du coup c'est l'aire

@pouvens

Oui c'est la réponse à la première question.

Cette fonction est définie sur l'ensemble des réels, mais si on tient compte de la position du point M; $x$ varie de 0 à 4.

Pour la question 3, tu résous l'équation $2x^2-8x+16=11$

du coup l'ensemble de définition est 0;4

@pouvens

Oui [0;4].

2x²-8x+16-11=0
2x²-8x+5=0

@pouvens

Résous cette équation du second degré.

@pouvens a dit dans les fonctions généralités :

2x²-8x+5=0
2(x²-4x+2)=0

@pouvens

Non,
$2x^2-8x+5=2(x^2-4x+2,5)$
Quelle méthode as tu dans le cours pour résoudre une équation du second degré ?
Factorisation ?
Méthode par le calcul du discriminant ?