L'encadrement de sinus
-
Rriro dernière édition par
Bonjour,
Mq pour tout x > 0; 2x + sin(x) > 0
-
Bonjour riro,
Une méthode, étudie les variations de la fonction f(x)=2x+sin(x)f(x) = 2x + sin(x)f(x)=2x+sin(x) pour x>0x\gt0x>0.
-
Kkane dernière édition par
On considère l'équation SIN3x= -SIN2x
1)a) Résoudre cette question dans IR puis dans ]-π,π]
b) Représenter les solutions sur le cercle trigonométrie
-
Bonjour kane,
Tu utilises la relation sin(x+π)=−sinxsin(x+\pi) = -sinxsin(x+π)=−sinx
donc l'équation à résoudre s'écrit : sin(3x)=sin(2x+π)sin(3x) = sin(2x+\pi)sin(3x)=sin(2x+π)
d'ou tu résous les équations
3x=2x+π+2kπ3x = 2x+\pi+2k\pi3x=2x+π+2kπ et
3x=π−2x−π+2kπ3x = \pi-2x-\pi + 2k\pi3x=π−2x−π+2kπindiques tes réponses si tu souhaites une correction.
-
mtschoon dernière édition par mtschoon

@kane , bonjour,
@kane , tu aurais dû ouvrir ta propre discussion car ta question n'a rien à voir avec celle posée par @riro
-
mtschoon dernière édition par mtschoon

Bonjour,
Consultation éventuelle pour détails de l'encadrement de 2x+sinx2x+sinx2x+sinx
Comme indiqué par @Noemi , le plus simple est d'étudier les variations de f définie par
f(x)=2x+sinxf(x)=2x+sinxf(x)=2x+sinxDérivée : f′(x)=2+cosxf'(x)=2+cosxf′(x)=2+cosx
Pour tout xxx réel, −1≤cosx≤+1-1\le cosx\le +1−1≤cosx≤+1 donc 1≤2+cosx≤31\le 2+cosx\le 31≤2+cosx≤3
Donc, f′(x)>0f'(x) \gt 0f′(x)>0 donc f strictement croissante sur R
Or, f(0)=2×0+sin0=0f(0)=2\times 0+sin0=0f(0)=2×0+sin0=0
Donc , pour x>0x\gt 0x>0, f(x)>0f(x) \gt 0f(x)>0 c'est à dire 2x+sinx>02x+sinx \gt 02x+sinx>0
Illustration avec la représentation graphique de f pour x positif
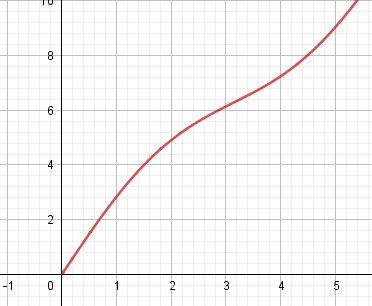
-
BBlack-Jack dernière édition par mtschoon
Bonjour mtschoon,
Petit soucis avec la ligne : " Or, f(x)=2×0+sin0=0f(x)=2\times 0+sin0=0f(x)=2×0+sin0=0"
Je présume que tu as voulu écrire f(0) = ...
mais, même ainsi, il resterait un petit soucis puisque f n'est pas définie en 0.Peut être avec lim(x --> 0+) f(x) = ...
Sauf mauvaise interprétation de ma part...
On peut aussi contourner l'obstacle en étudiant f(x) = 2x + sin(x) pour x >= 0 et tirer les conclusions en excluant au final 0 du domaine de f(x).
-
mtschoon dernière édition par

Bien vu !
Faute de frappe modifiée .
-
mtschoon dernière édition par mtschoon

Pour plus de précisions si nécessaire,
Sur R, f définie par f(x)=2x+sin(x)f(x)=2x+sin(x)f(x)=2x+sin(x), est définie, dérivable donc continue (Théorème) et strictement croissante (car f′(x)>0f'(x)\gt 0f′(x)>0)
De plus, f(0)=0f(0)=0f(0)=0,D'où tableau de variations
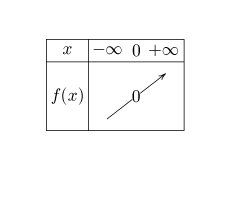
D'où conclusion.