Équations Trigonométriques

[TheoG]

Bonjour,
Je rencontre actuellement des problèmes pour faire mes exercices, mon enseignante ma donné deux équation à résoudre sauf que je n'y arrive pas du tout(Son cours n'est pas terrible).
Jai beau chercher sur Internet un cours je ne trouve rien.
De mon côté jai essayé de faire le début des équations et ça donne sa.

Sin(4t+π/6) =1/2
4t+π/6=π/3
4t=π/6-π/3
Première équations je n'arrive pas à aller plus loins

Cos(3t+π) =1/2
3t+π=1/2
3t=π-2
Voici ce que j'ai commencé à faire pour la deuxième...

Merci de m'aider ça me serais utile.
Cordialement.
Merci

[Noemi]

Bonjour Theo-Garces,

As-tu dans le cours une méthode de résolution des équations du type :
$sin(x)=sin(a)$ et
$cos(x)=cos(a)$ ?

[TheoG]

@Noemi Bonjour non je n'ai rien de tout ça c'est sa mon problème

[Noemi]

@TheoG

Tu résous donc les équations trigonométriques à l'aide du cercle trigonométrique ?

[TheoG]

@Noemi Oui je dois me référer à ce cercle

[Noemi]

@TheoG

Pour l'équation $sin(4t+\frac{\pi }{6})=\frac{1}{2}$

1. Détermine à l'aide du cercle trigonométrique pour quel(s) angle(s) (en radians) le sinus est égal à $\frac{1}{2}$. Tu dois trouver deux valeurs $\frac{\pi }{6}$ et $\frac{5\pi }{6}$.
2. Tu résous ensuite les équations $4t+\frac{\pi }{6}=\frac{\pi }{6}+2k\pi$ et $4t+\frac{\pi }{6}=\frac{5\pi }{6}+2k\pi$.

[TheoG]

@Noemi d'accord merci

[TheoG]

@Noemi mais est ce que mon raisonnement du début et bien ou totalement faux ? 🧐

[Noemi]

@TheoG

La deuxième équation donne $4t=\frac{2\pi }{3}+2k\pi$
d'ou $t=\frac{\pi }{6}+\frac{k\pi }{2}$

Indique tes éléments de réponse si tu souhaites une correction.

[Noemi]

@TheoG

Ton raisonnement est faux car tu as indiqué $\frac{\pi }{3}$ au lieu de $\frac{\pi }{6}$.
et tu n'as pas indiqué l'autre solution.

Pour déterminer les deux solutions sur le cercle trigonométrique, tu places $\frac{1}{2}$ sur l'axe des sinus et tu traces une horizontale. Elle coupe le cercle trigonométrique en deux points, tu détermines alors les valeurs correspondantes des angles.

[mtschoon]

Bonjour,

Cercle trigonométrique pour illustrer la démarche demandée par @TheoG

Pour la première équation, suivre les indications de @Noemi
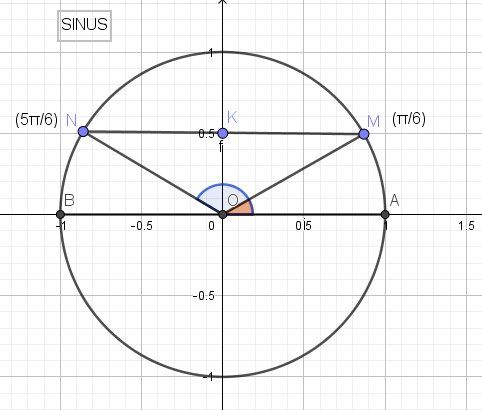
On place le point K (0, 1/2) sur l'axe des sinus (axe des ordonnées).
On en déduit la place de M et N (points du cercle trigonométrique d'ordonnée 1/2)

Une mesure de $(\overrightarrow{OA}\overrightarrow{OM})$ est , en radians, $\frac{\pi }{6}$ (c'est à dire 30 °)
L'ensemble des mesures de $(\overrightarrow{OA}\overrightarrow{OM})$ est , en radians, $\frac{\pi }{6}+2k\pi$ , avec $k\in Z$

Une mesure de $(\overrightarrow{OA}\overrightarrow{ON})$ est , en radians, $\pi -\frac{\pi }{6}=\frac{5\pi }{6}$ (c'est à dire 120 °)
L'ensemble des mesures de $(\overrightarrow{OA}\overrightarrow{ON})$ est , en radians, $\frac{5\pi }{6}+2k\pi$ , avec $k\in Z$

On résout , comme indiqué :
$4t+\frac{\pi }{6}=\frac{\pi }{6}+2k\pi$
et
$4t+\frac{\pi }{6}=\frac{5\pi }{6}+2k\pi$

On obtient, comme indiqué, après calculs
$t=\frac{k\pi }{2}$
et
$t=\frac{\pi }{6}+\frac{k\pi }{2}$

[mtschoon]

De même, cercle trigonométrique pour illustrer la démarche demandée par @TheoG pour la seconde équation

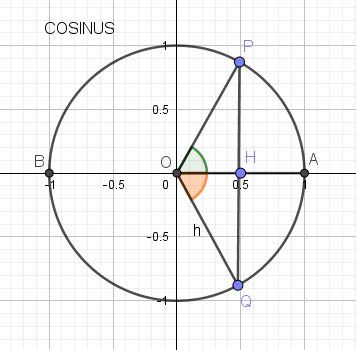
On place le point H (1/2 , 0) sur l'axe des cosinus (axe des abscisses).
On en déduit la place de P et Q (points du cercle trigonométrique d'abscisse 1/2)

Une mesure, en radians, de $(\overrightarrow{OA},\overrightarrow{OP)}$ est $\frac{\pi }{3}$ (60°)
L'ensemble des mesure, en radians, de $(\overrightarrow{OA},\overrightarrow{OP)}$ est $\frac{\pi }{3}+2k\pi$ avec $k\in Z$

Une mesure, en radians, de $(\overrightarrow{OA},\overrightarrow{OQ)}$ est $-\frac{\pi }{3}$ (60°)
L'ensemble des mesure, en radians, de $(\overrightarrow{OA},\overrightarrow{OQ)}$ est $-\frac{\pi }{3}+2k\pi$ avec $k\in Z$

On résous donc :

$3t+\pi =\frac{\pi }{3}+2k\pi$
et
$3t+\pi =-\frac{\pi }{3}+2k\pi$

On obtient donc, après calculs, sauf erreur,

$t=-\frac{2\pi }{9}+\frac{2k\pi }{3}$
et
$t=-\frac{4\pi }{9}+\frac{2k\pi }{3}$

[TheoG]

@mtschoon Merci beaucoup de votre aide

[mtschoon]

@TheoG de rien !

J'espère que c'est assez clair, mais reposte si tu as besoin.