On sait que sin(5x)=16sin^5x-20sin^3x+5sinx
-
Kkane dernière édition par mtschoon
On sait que Sin(5x)=16sin5x−20sin³x+5sinxSin(5x)=16sin^5x -20sin³x+5sinxSin(5x)=16sin5x−20sin³x+5sinx
Résoudre dans IR sin(5x)=0; vérifier que π\5 et 2π\5 sont des solutions de cette équation
-
Bonjour kane, (Marque de politesse à ne pas oublier !!)
Pour la résolution de sin(5x)=0sin(5x) = 0sin(5x)=0 applique le cours,
soit à résoudre
5x=0+2kπ5x = 0 + 2k\pi5x=0+2kπ et
5x=π+2kπ5x= \pi+2k\pi5x=π+2kπ.
-
BBlack-Jack dernière édition par
Bonjour,
Je parierais que l'énoncé n'est pas complet ... sinon, à quoi servirait l'info : "On sait que SIN5x=16SIN^5-20SIN³x+5SINx"
Le but final est probablement de trouver les valeurs "justes" de sin(Pi/5) et de sin(2Pi/5)
Si oui, il faut alors résoudre l'équation 16.SIN^5(x) - 20.SIN³(x) + 5.SIN(x) = 0 ... en trouvant toutes les valeurs de sin(x) qui satisfont l'équation.
Assez facile, en mettant sin(x) en facteur et puis en constatant que le suite est une équation bicarrée et ...
Et ensuite en réfléchissant quelles valeurs de sin(x) solutions de 16.SIN^5(x) - 20.SIN³(x) + 5.SIN(x) = 0 correspondent à sin(Pi/5) et sin(2Pi/5)
-
mtschoon dernière édition par mtschoon

Bonjour,
Seulement une information
Cet énoncé ancien figure sur plusieurs sites...avec la formulation que j'indique :1- En remarquant que sin 5x = sin (4x+x) démontrer que sin 5x = 16 sin^5x - 20 sin^3x + 5sin x
2- Résoudre dans R l'équation sin 5x = 0, vérifier que pi/5 et 2pi/5 sont solutions de cette équation
3-Résoudre dans R l'équation 16X^5 - 20X^3 + 5X = 0
4- En déduire des questions précédentes les valeurs de sin (pi/5) et sin(2pi/5)
-
mtschoon dernière édition par mtschoon

Bonjour,
@kane a posé un énoncé très incomplet et ne semble pas (encore) avoir consulté les informations données...
Quelques pistes pour consultations éventuelles.
QUESTION 1)
Utilisation de la formule d'addition
sin(a+b)=sinacosb+sinbcosasin(a+b)=sinacosb+sinbcosasin(a+b)=sinacosb+sinbcosa
d'où
sin(5x)=sin(4x+x)=sin4xcosx+sinxcos4x\boxed{sin(5x)=sin(4x+x)=sin4xcosx+sinxcos4x}sin(5x)=sin(4x+x)=sin4xcosx+sinxcos4xUtilisation des formules de duplication
sin(2a)=2sinacosasin(2a)=2sinacosasin(2a)=2sinacosa
cos(2a)=1−2sin2acos(2a)=1-2sin^2acos(2a)=1−2sin2a
et de la formule de base cos2a=1−sin2acos^2a=1-sin^2acos2a=1−sin2asin4xcosx=2sin2xcos2xcosx=2(2sinxcosx)(1−2sin2x)cosxsin4xcosx=2sin2xcos2xcosx=2(2sinxcosx)(1-2sin^2x)cosxsin4xcosx=2sin2xcos2xcosx=2(2sinxcosx)(1−2sin2x)cosx
d'où
sin4xcosx=4sinxcos2x(1−2sin2x)=4sinx(1−sin2x)(1−2sin2x)sin4xcosx=4sinxcos^2x(1-2sin^2x)=4sinx(1-sin^2x)(1-2sin^2x)sin4xcosx=4sinxcos2x(1−2sin2x)=4sinx(1−sin2x)(1−2sin2x)Après développement et regroupement
sin4xcosx=4sinx−12sin3x+8sin5x\boxed{sin4xcosx=4sinx-12sin^3x+8sin^5x}sin4xcosx=4sinx−12sin3x+8sin5xAvec le même principe
cos4xsinx=[1−2sin2(2x)]sinx=sinx−2sin2(2x)sinxcos4xsinx=[1-2sin^2(2x)]sinx=sinx-2sin^2(2x)sinxcos4xsinx=[1−2sin2(2x)]sinx=sinx−2sin2(2x)sinx
cos4xsinx=sinx−2(2sinxcosx)2sinxcos4xsinx=sinx-2(2sinxcosx)^2sinxcos4xsinx=sinx−2(2sinxcosx)2sinx
cos4xsinx=sinx−8sin2xcos2xsinxcos4xsinx=sinx-8sin^2xcos^2xsinxcos4xsinx=sinx−8sin2xcos2xsinx
cos4xsinx=sinx−8sin2x(1−sin2x)sinxcos4xsinx=sinx-8sin^2x(1-sin^2x)sinxcos4xsinx=sinx−8sin2x(1−sin2x)sinxAprès développement et regroupement
cos4xsinx=sinx−8sin3x+8sin5x\boxed{cos4xsinx=sinx-8sin^3x+8sin^5x}cos4xsinx=sinx−8sin3x+8sin5xConclusion, en regroupant les deux expressions trouvées
sin(5x)=16sin5x−20sin3x+5sinx\boxed{sin(5x)=16sin^5x-20sin^3x+5sinx}sin(5x)=16sin5x−20sin3x+5sinx
-
mtschoon dernière édition par mtschoon

QUESTION 2)
Sin(5x)=0\boxed{Sin(5x)=0}Sin(5x)=0
1er cas :
Pour k∈Zk \in Zk∈Z : 5x=0+2π5x=0+2\pi5x=0+2π <=> 5x=2kπ5x=2k\pi5x=2kπ <=> x=2kπ5\boxed{x=\dfrac{2k\pi}{5}}x=52kπ
Les solutions sur [0,2π[[0,2\pi[[0,2π[ sont
0,2π5,4π5,6π5,8π5\boxed{0,\dfrac{2\pi}{5},\dfrac{4\pi}{5},\dfrac{6\pi}{5},\dfrac{8\pi}{5}}0,52π,54π,56π,58π
Points images sur le cercle trigonométrique : points A, C, E, G, I.2ème cas :
Pour k∈Zk \in Zk∈Z : 5x=π+2π5x=\pi+2\pi5x=π+2π <=> x=π5+2kπ5\boxed{x=\dfrac{\pi}{5}+\dfrac{2k\pi}{5}}x=5π+52kπ
Les solutions sur [0,2π[[0,2\pi[[0,2π[ sont
π5,3π5,π,7π5,9π5\boxed{\dfrac{\pi}{5},\dfrac{3\pi}{5},\pi,\dfrac{7\pi}{5},\dfrac{9\pi}{5}}5π,53π,π,57π,59π
Points images sur le cercle trigonométrique : points B, D, F, H, J.Conclusion : mis dans l'ordre croissant, les solutions sur [0,2π[[0,2\pi[[0,2π[ sont
0,π5,2π5,3π5,4π5,π,6π5,7π5,8π5,9π5\boxed{0, \dfrac{\pi}{5}, \dfrac{2\pi}{5}, \dfrac{3\pi}{5}, \dfrac{4\pi}{5}, \pi, \dfrac{6\pi}{5}, \dfrac{7\pi}{5}, \dfrac{8\pi}{5}, \dfrac{9\pi}{5}}0,5π,52π,53π,54π,π,56π,57π,58π,59π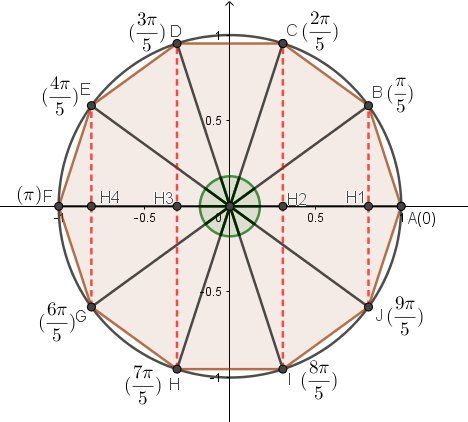
-
mtschoon dernière édition par mtschoon

QUESTION 3)
16X5+20X2+5X=016X^5+20X^2+5X=016X5+20X2+5X=0 <=> X(16X4−20X2+5)=0X(16X^4-20X^2+5)=0X(16X4−20X2+5)=0
1er cas : X=0X=0X=0
2ème cas 16X4−20X2+5=016X^4-20X^2+5=016X4−20X2+5=0
Equation bicarrée.
Changement de variable X2=YX^2=YX2=YEquation auxiliaire : 16Y2−20Y+5=016Y^2-20Y+5=016Y2−20Y+5=0
équation du second degré à résoudre.
solutions : Y1=5+58Y_1=\dfrac{5+\sqrt 5}{8}Y1=85+5 et Y2=5−58Y_2=\dfrac{5-\sqrt 5}{8}Y2=85−5Retour à X:
X1,2=±5+58=±10+2516=±10+254X_{1,2}=\pm \sqrt{\dfrac{5+\sqrt 5}{8}}=\pm \sqrt{\dfrac{10+2\sqrt 5}{16}}=\pm\dfrac{\sqrt{10+2\sqrt 5}}{4}X1,2=±85+5=±1610+25=±410+25
X3,4=±5−58=±10−2516=±10−254X_{3,4}=\pm \sqrt{\dfrac{5-\sqrt 5}{8}}=\pm \sqrt{\dfrac{10-2\sqrt 5}{16}}=\pm\dfrac{\sqrt{10-2\sqrt 5}}{4}X3,4=±85−5=±1610−25=±410−25Les solutions, mises dans l'ordre croissant, sont :
−10+254,−10−254,0,10−254,10+254\boxed{-\dfrac{\sqrt{10+2\sqrt 5}}{4}, -\dfrac{\sqrt{10-2\sqrt 5}}{4},0,\dfrac{\sqrt{10-2\sqrt 5}}{4},\dfrac{\sqrt{10+2\sqrt 5}}{4}}−410+25,−410−25,0,410−25,410+25
-
mtschoon dernière édition par mtschoon

QUESTION 4
Conséquence des 3 premières questions.En posant X=sinxX=sinxX=sinx, l'équation de la question 3) se transforme en
16sin5x−20sin3x+5sinx=016sin^5x-20sin^3x+5sinx=016sin5x−20sin3x+5sinx=0
Les valeurs de sinxsinxsinx satisfaisant à cette première équation sont donc les 5 valeurs trouvées à la question 3)Vu l'égalité démontrée à la question 1), les valeurs de xxx correspondantes sont les 10 valeurs trouvées à la question 2), dont π5\dfrac{\pi}{5}5π et 2π5\dfrac{2\pi}{5}52π font partie.
En analysant les schéma du cercle trigonométrique , avec les mesures des 10 angles et les sinus (représentés en pointillés rouges), on peut tirer les conclusions :
sin(π5)=H1B‾sin(\dfrac{\pi}{5})=\overline{H_1B}sin(5π)=H1B. C'est la plus petite valeur positive des sinus-solutions , donc
sin(π5)=10−254\boxed{sin(\dfrac{\pi}{5})=\dfrac{\sqrt{10-2\sqrt 5}}{4}}sin(5π)=410−25
sin(2π5)=H2C‾sin(\dfrac{2\pi}{5})=\overline{H_2C}sin(52π)=H2C. C'est la plus grande valeur positive des sinus-solutions, donc
sin(2π5)=10+254\boxed{sin(\dfrac{2\pi}{5})=\dfrac{\sqrt{10+2\sqrt 5}}{4}}sin(52π)=410+25
Complément non demandé dans l'exercice
On continuant l'analyse, on peut déterminer la valeur des sinus des autres angles.
.
sin(3π5)=10+254sin(\dfrac{3\pi}{5})=\dfrac{\sqrt{10+2\sqrt 5}}{4}sin(53π)=410+25
sin(4π5)=10−254sin(\dfrac{4\pi}{5})=\dfrac{\sqrt{10-2\sqrt 5}}{4}sin(54π)=410−25
sin(π)=0sin(\pi)=0sin(π)=0
sin(6π5)=−10−254sin(\dfrac{6\pi}{5})=-\dfrac{\sqrt{10-2\sqrt 5}}{4}sin(56π)=−410−25
sin(7π5)=−10+254sin(\dfrac{7\pi}{5})=-\dfrac{\sqrt{10+2\sqrt 5}}{4}sin(57π)=−410+25
sin(8π5)=−10+254sin(\dfrac{8\pi}{5})=-\dfrac{\sqrt{10+2\sqrt 5}}{4}sin(58π)=−410+25
sin(9π5)=10−254sin(\dfrac{9\pi}{5})=\dfrac{\sqrt{10-2\sqrt 5}}{4}sin(59π)=410−25Bonne lecture éventuelle.