AIDE PROBABILITÉ TERMINALE S

Bonjour, si quelqu'un peut m'aider à résoudre cet exercice je lui en serait reconnaissante.

L'étude commandée par un gérant conduit à la modélisation suivante :

parmi les clients ayant choisi de passer à une borne automatique, 65 % attendent moins de 12 minutes
parmi les clients passant en caisse, 84 % attendent moins de 12 minutes

On choisit un client au hasard et on définit les évenements suivants :
B: " le client paye à une borne automatique"
B(BARRE): " le client paye à une caisse avec opérateur"
S : "la durée d'attente du client lors du payement est inférieure à 12 minutes"

Une attente à 12 minutes à une caisse avec opérateur ou à une borne automatique engendre chez le client une percetion négative du magasin. Le gérant souhaite que 79% des clients attendent moins de 12 minutes.

Quelle est la proportion minimale de clients qui doivent choisir une borne automatique de paiement pour que cet objectif soit atteint ?

@mimims , bonjour,

Je trouve tes données très bizarres.
Il faut les vérifier.
Je pense que tu as mélangé les données de la borne automatique avec celles de la caisse avec opérateur.
Avec les probabilités que tu donnes, ce n'est plus une proportion minimale que l'on cherche mais une proportion maximale ! ! ! !

Principe :

Un arbre probabiliste peut clarifier l'énoncé.
Je t'en joins un, à compléter (il faut mettre p sur la branche B) r.

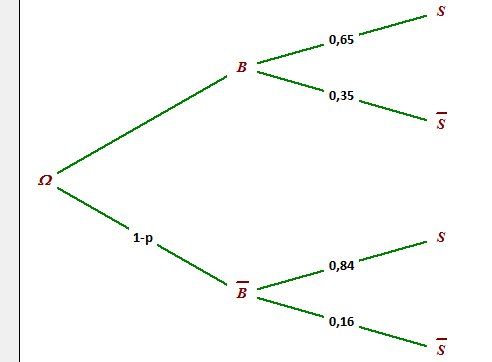
J'ai utilisé les probabilités que tu indiques
p est la probabilité qu'un client paye à une borne automatique
donc 1-p est la probabilité qu'un client paye à une caisse avec opérateur.
$P (B) = p$
$P(Bˉ)=1−pP(\bar B)=1-p$

Lorsque tu as bien fait l'arbre (en modifiant certainement les probabilités ...), tu l'utilises pour résoudre $\ge 0.79$

Le même type d'énoncé fait partie d'un exercice de Bac que je te joins, avec des données cohérentes avec la question posée.
Tu peux consulter (Bac 2018 S Amérique Nord)
http://www.matheatre.fr/Maths/Div/Annales/2018/2018_05_S_AmNor_Cor-2.pdf

Merci beaucoup pour votre aide !

@mimims ,

De rien (et j'espère que tu as bien modifié les données)