étudier les fonctions
-
Jjuliette67 dernière édition par
bonjour, je suis en seconde, j'aurais besoin d'aide en maths sur les fractions,
on considère les fonctions f et g definies sur R
f (x) = 5x + 3 et g = -2x + 7
1)-résoudre f (x) = 0
-déterminer les variations de f- déterminer le tableau de signes de f(x)
-
- reprendre les questions précédentes pour g (x)
-
Bonjour juliette67,
Pour la première question :
résous l'équation 5x+3=05x+3 = 05x+3=0
soit 5x+3−3=0−35x+ 3 - 3 = 0 -35x+3−3=0−3 ou
5x=−35x= -35x=−3
x=.....x = .....x=.....Pour les variations, utilise le cours.
Pour une fonction f(x)=ax+bf(x) = ax+bf(x)=ax+b,
si a<0a \lt0a<0 la fonction est décroissante
si a>0a \gt0a>0 la fonction est croissante.Pour la fonction fff, a=5a= 5a=5 donc .....
-
mtschoon dernière édition par

Bonjour,
@juliette67 , un petit plus, si besoin
Après calcul, f(x)=0f(x)=0f(x)=0 <=> 5x=−35x=-35x=−3 <=> x=−35x=-\dfrac{3}{5}x=−53
f(x) est de la forme f(x)=ax+bf(x)=ax+bf(x)=ax+b
Ici, a=5a=5a=5 donc a>0a \gt 0a>0 donc f croissante.Tu peux donc faire la tableau de variations:
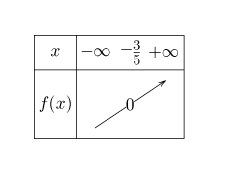
Conséquence sur le signe de f(x)
Pour x<−35x\lt-\dfrac{3}{5}x<−53 , f(x)<0f(x) \lt 0f(x)<0 c'est à dire f(x) négatif
Pour x>−35x\gt-\dfrac{3}{5}x>−53 , f(x)>0f(x) \gt 0f(x)>0 c'est à dire f(x) positifTu raisonnes de la même façon pour g(x)=−2x+7g(x)=-2x+7g(x)=−2x+7 , mais cette fois , a est négatif (a=-2)
Tu dois trouver g(x)=0g(x)=0g(x)=0 <=> x=72x=\dfrac{7}{2}x=27
Vu que a<0a \lt 0a<0 , g est décroissante.
Tu en tires les conclusions nécessaires.
Bon travail.