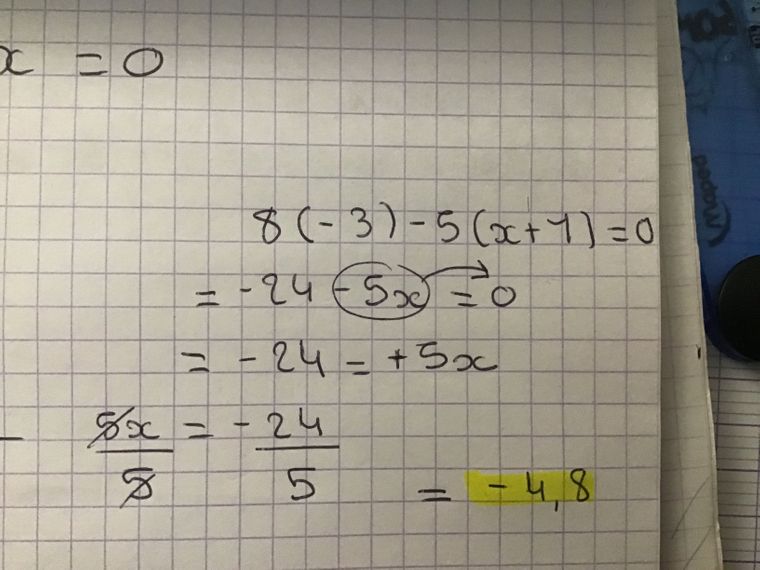Vecteurs mathématiques

Bonjour, je galère sur cet exercice de math: si vous pourriez m’aider

Soient les points A(-1 ; 3), B(7 ; et C(2 ; 4).

Soit 𝑀(𝑥; 0) un point de l’axe des abscisses. Calculer 𝑥 pour que A, B et M soient
alignés.
Soit 𝑁(0; 𝑦) un point de l’axe des ordonnées. Calculer 𝑦 pour que les droites (AB) et (CD) soient parallèles.

Merci beaucoup!

@lauryne_b , bonjour,

Faute de frappe certainement...Indique l'ordonnée de B

@lauryne_b
Petite erreur: B (7;8) et C ...

@lauryne_b ,

D'accord pour B mais à la seconde question , tu parles d'un point D dont tu ne donnes pas les coordonnées.
Merci de compléter.

Bonjour lauryne_b,

Utilise les coordonnées des vecteurs $AB→\overrightarrow{AB}$ et $AM→\overrightarrow{AM}$ .

@mtschoon
Justement l’exercice ne les donnent pas

@Noemi
Pour les coordonné de AB (8;5) mais pour AM du coup je reste bloquer à AM | x-(-1) et 3

@lauryne_b ,

Piste pour la 1)

Tu calcules (X,Y) les coordonnées de $AB→\overrightarrow{AB}$
$X=x_B-x_A=8$
$Y=y_B-y_A=5$

De même, tu calcules les coordonnées (X',Y')de $AM→\overrightarrow{AM}$
$X'=x_M-x_A=x+1$
$Y'=y_M-y_A=0-3=-3$

Vecteurs colinéaires <=> déterminant nul <=> XY'-YX'=0

Tu trouves une équation d'inconnue x à résoudre.

@mtschoon
Donc en calculant le déterminant je suis arrivé à cette équation : 8 * (-3) - 5 * 1x = -24 - 5x
C’est bien cette équation à résoudre ?

@lauryne_b ,

Il y a peut-être une faute de frappe...

C'est $(8) (- 3) - (5) (x + 1) = 0$

@mtschoon
Oui je me suis trompé, d’accord j’essaie de résoudre ça

@lauryne_b ,

Après calcul, sauf erreur, tu dois trouver

$x=−295x=\dfrac{-29}{5}$

Pour vérifier, tu peux placer M ainsi trouvé sur ton graphique et t'assurer que A,B,M sont bien alignés.

Quand tu auras résolu la 1, regarde à nouveau l'énoncé de la 2) au sujet de ce point D
C'est peut-être N à la place de D, ce qui serait logique...

Tu pourras ainsi utiliser la même démarche qu'à la question 1) (vecteurs colinéaires)

@mtschoon je n’arrive pas à trouver comme vous quand je résous

@lauryne_b ,

Tu développes et tu simplifies :

$8 (- 3) - 5 (x + 1) = 0$ <=> $- 24 - 5 x - 5 = 0$ <=> $- 29 - 5 x = 0$

Tu transposes :

$- 5 x = 29$

Tu termines en divisant par -5

@mtschoon
Oui j’ai trouvé, mais quand on calcule le deternminent en remplaçant x par -5,8, on n’a pas un résultat nul

@mtschoon

Je pense que c’est ça car avec ce résultat ça fonctionne

@lauryne_b ,

Je fais la vérification.

$8(−3)−5(−−295+1)=−24−5(−29+55)8(-3)-5(-\dfrac{-29}{5}+1)=-24-5(\dfrac{-29+5}{5})$

c'est à dire

$−24−5(−245)=−24+24=0-24-5(\dfrac{-24}{5})=-24+24=0$

CQFD

Exact , je vois ce que tu veux dire (faute de frappe).
$x=−245=−4.8x=-\dfrac{24}{5}=-4.8$

Tout à l'air bon, je pense que tu peux passer à la seconde question en mettant N à la place de D.

Tiens nous au courant si besoin.

@lauryne_b ,

Je te démarre la seconde question,

$AB→\overrightarrow{AB}$ déjà calculé : $X = 8$ et $Y = 5$

$CN→\overrightarrow{CN}$ :
$X'=x_N-x_C=0-2=-2$
$Y'=y_N-y_C=y-4$

Tu utilises à nouveau $X Y^{'} - Y X^{'} = 0$

@mtschoon
C’est le même principe que la première non ?

@lauryne_b ,

Oui, regarde le début que je viens de te donner (nos posts ont dû se croiser)

Sauf erreur, tu dois trouver pour cette seconde question (en remplaçant D par N) :
$y=114y=\dfrac{11}{4}$

@mtschoon
Donc l’équation c’est 8* ( y - 4 )- 5* (-2) ?

Oui, en écrivant ....=0

@mtschoon ok j’essaie

@mtschoon
Bon je suis bloqué -_-

@mtschoon
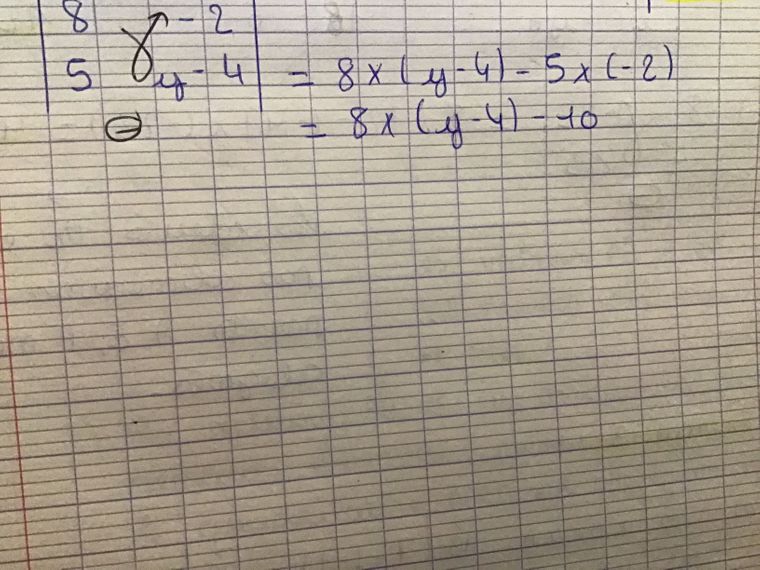
J’ai essayé plusieurs fois au brouillon mais ici je ne sais plus quoi faire

@lauryne_b ,

Je ne sais pas où tu bloques...

$8 (y - 4) - 5 (- 2) = 0$

En développant

$8 y - 32 + 10 = 0$

Essaie de continuer

@lauryne_b ,

Nos postes se sont encore croisés !

Dans ce tu tu viens de mettre, je vois une faute de signe car $- 5 (- 2) = + 10$ ( tu as écrit -10)

@mtschoon
Ah oui en développent !! Ok j’avais pas compris

@lauryne_b ,

Es-tu arrivé à $y=228=114=2.75y=\dfrac{22}{8}=\dfrac{11}{4}=2.75$ ?

@lauryne_b
Oui j’ai trouver ça !

@lauryne_b .

C'est très bien !

@mtschoon
Mon exercice est terminé, je te remercie vraiment de ta patience, j’ai tout compris Passez une bonne journée et bon courage

C'est avec plaisir @lauryne_b que nous t'aidons.

Reviens si tu as de nouvelles difficultés.