Dimensions d'un champ rectangulaire (Second degré)
-
Ccassandrabaloo dernière édition par mtschoon
Bonjour j'ai un 2 exercices de Math à rendre mais je n'y arrive pas.
- on doit entourer un champ rectangulaire et le diviser en 2 parties à l'aide d'une clôture parallèle à un des côtés. Trouver les dimensions du champs d'aire maximum que l'on peut entourer et diviser avec un rouleau de 1200m.
(Réponse en semaine)
Merci beaucoup
(énoncé du second exercice supprimé par la modération)
-
Bonjour cassandrabaloo,
Un seul exercice par post.
- pose les inconnues du problème et écris les équations correspondant à l'énoncé.
Si xxx et yyy sont les dimensions du champ.
L'aire du champ A=xyA = xyA=xy
Dimension de la clôture 3x+2y=12003x+2y= 12003x+2y=1200
Tu isoles yyy de la deuxième relation en fonction de xxx
Que tu remplaces dans l'expression de l'aire.
...
As-tu fait un schéma ?
Pose une question si tu ne comprends pas les indications.
- pose les inconnues du problème et écris les équations correspondant à l'énoncé.
-
Ccassandrabaloo dernière édition par
@Noemi merci pour les infos j'ai fais mon exercices et je suis tombée sur les bonnes réponses merci
-
Comment as-tu déterminé le maximum ?
-
mtschoon dernière édition par mtschoon

Bonjour,
@cassandrabaloo a posté en 4ème.
En consultant son adresse IP, je constate que @cassandrabaloo poste de Belgique.
Il y a donc une confusion dans les rubriques...
@cassandrabaloo doit savoir étudier une fonction polynôme du second degré.
Il faut donc mettre ce topic dans une rubrique Lycée (ou bien "Seconde" ou bien "Première" suivant que les dérivées sont connues ou pas ...)
A tout hasard, je l'ai mis en "Seconde". ainsi que l'autre topic de @cassandrabaloo .
-
mtschoon dernière édition par mtschoon

Bonjour,
Un petit plus pour ceux qui voudraient faire cet exercice , en cette période où les cours n'ont pas lieu.
Schéma pour illustrer la situation
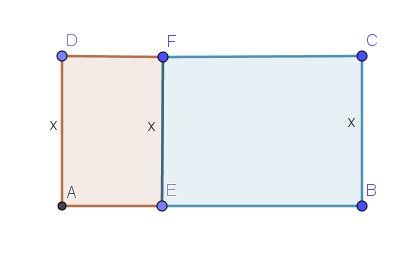
AB=CD=yAB=CD=yAB=CD=y
AD=EF=BC=xAD=EF=BC=xAD=EF=BC=xEn utilisant les pistes de @Noemi relatives au rouleau de 1200 m :
3x+2y=12003x+2y=12003x+2y=1200 <=>y=600−1.5xy=600-1.5xy=600−1.5xL'aire du champ vaut : A=xyA=xyA=xy
donc : A=f(x)=x(600−1.5x)=−1.5x2+600xA=f(x)=x(600-1.5x)=\boxed{-1.5x^2+600x}A=f(x)=x(600−1.5x)=−1.5x2+600x
f est une fonction polynôme du second degré dont les variations sont à étudier avec la méthode vue en cours (donc Voir le cours)
Conséquence :
Sur [0,400], on obtient la représentation graphique :
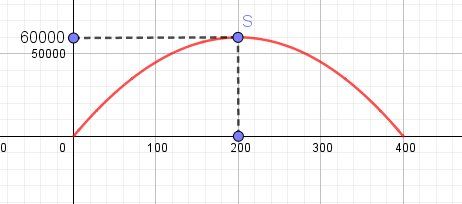
Conclusion :
L'aire maximale (60000 m²) est obtenue pour x=200x=200x=200.
On en déduit que , pour cette aire maximale, y=600−1.5(200)=300y=600-1.5(200)=300y=600−1.5(200)=300