les vecteurs exercices 2

bonjour vous pouvez m'aider svp

soient M(-2;5) et N(3;2)
alors le vecteur MN a pour coordonnées
quelle est la norme du vecteur u (-4)?
3
quelle valeur faut donner à x pour que les vecteurs u (2) et v (-6) soient colinéaires? 3 x
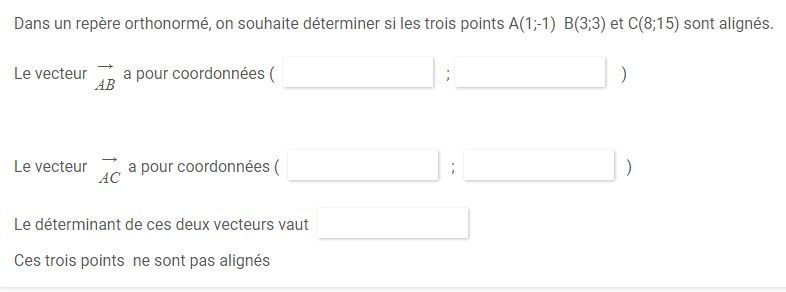
dans un repère orthonormé , on souhaite déterminer si les points A(1;1) B(3;3) et C (8;15) sont alignés.
le vecteur AB a pour coordonnées
le vecteur AC a pour coordonnées
le déterminant de ces deux vecteurs sont
ces trois points ne sont pas alignés
5)soient A(-2;3) , B(6;-1) , C(1;2), et D(5;0).Les droites (AB) et (CD) sont elles parallèles?
les coordonnées du vecteur AB sont
les coordonnées du vecteur CD sont
donc vecteur AB= CD
donc les droites sont parallèles.

Bonjour pouvens,

Je t'ai indiqué la méthode pour les question 1 et 2.
Indique tes éléments de réponse.

MN=(1;3)

@pouvens

$MN→=(xN−xM;yN−yM)=.....\overrightarrow{MN}= (x_N-x_M ;y_N-y_M) = .....$

@pouvens a dit dans les vecteurs exercices 2 :

soient M(-2;5) et N(3;2)
MN=(-2-3;5-2)=(-5;3)

@pouvens

Tu ne respectes pas l'ordre des termes
$;−3)\overrightarrow{MN}= (x_N-x_M ;y_N-y_M) = (3-(-2) ; 2-5) = (5\ ;-3)$
La norme du vecteur $u→\overrightarrow{u}$ est égale à $xu2+yu2\sqrt{x_{u}^2+y_{u}^2}$

racine de 25=5

@pouvens

C'est juste.

question 3. Les vecteurs $u→:(x;y)\overrightarrow{u} : (x;y)$ et $v→:(x′;y′)\overrightarrow{v} : (x';y')$ sont colinéaires si
$x y^{'} - x^{'} y = 0$ ou si $x y^{'} = x^{'} y$ .

donc x=-9

@pouvens

C'est correct.

Question 4. détermine les coordonnées des vecteurs et
vérifie l'énoncé de cette question. Il est incomplet.

j'ai que ça

AB=(-2;2)
AC=(-7;-14)

@pouvens

Toujours des erreurs de signes
$AB→=(3−1;3−1)=(2;2)\overrightarrow{AB}=(3-1;3-1) = (2;2)$
et $AC→=(8−1;15−1)=(7;14)\overrightarrow{AC}=(8-1;15-1) = (7;14)$