Exprimer une aire en fonction de x et déterminer quelle valeur de x est égale au disque et à la partie hachurée

[Smile Shadow]

Bonjour je suis bloquée sur cet exercice depuis hier

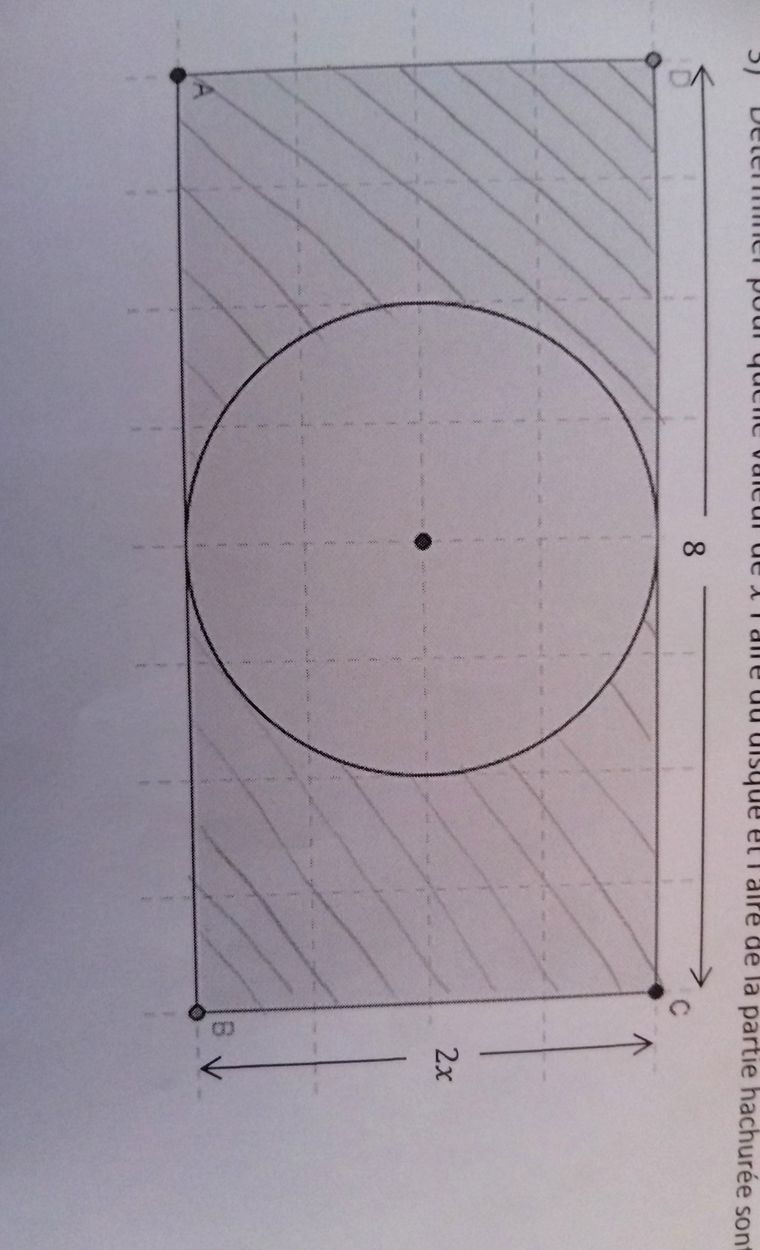
Sur la figure ci-dessous, x désigne un nombre strictement positif. Le disque et le rectangle ont même centre et le cercle est tangent à deux côtés opposés du rectangle.

1. Exprimer l'aire du disque en fonction de x.
2. Exprimer l'aire de la partie hachurée en fonction de x.
   Indication : Commencer par exprimer l'aire de la partie hachurée en fonction de l'aire du rectangle et de l'aire du disque.
3. Déterminer pour quelle valeur de x l'aire du disque et l'aire de la partie hachurée sont égales.
   
   Pour le 1 j'ai trouver pour l'aire 4 X Pi = 12,6 arrondi au dixième près.
   Pour le 2 j'ai trouver comme aire du rectangle 8X 2x = 16x
   du coup j'ai fais 12,6-16x. Mais à présent je ne sais plus quoi faire, pourriez vous m'expliquez comme faire s'il vous plait

[Noemi]

Bonjour Smile-Shadow,

Pour la question 1, il faut exprimer l'aire en fonction de $x$.

[mtschoon]

@Smile-Shadow , bonjour

Je regarde tes réponses.

Question 1)

le disque a pour rayon $R=x$
Son aire vaut donc $\pi R^2=\pi x^2$

Question 2)

Oui pour l'aire du rectangle $16x$
L'aire de la partie hachurée est donc :$16x-\pi x^2$

Question 3)

Tu dois résoudre, pour $x>0$, l'équation
$\pi x^2=16x-\pi x^2$

Tu transposes dans le membre de gauche, ce qui te donne
$\pi x^2-16x+\pi x^2=0$ c'est à dire
$2\pi x^2-16x=0$.

Tu peux mettre $2x$ en facteur et terminer la résolution .
(Conserve la valeur exacte $\pi$, ainsi tu obtiendras une solution exacte).

Donne ta réponse si tu veux une vérification.

[Smile Shadow]

@mtschoon Bonjour,
Du coup en suivant votre raisonnement , j'ai fait:
Pi x^2 = 16x - Pi x^2 (j'ai alors enlever de chaque côté le x^2)
Pi = 16x - Pi (j'ai du coup soustrait par Pi )
0 = 16x
C'est faux, non ?

[mtschoon]

@Smile-Shadow ,

Ta démarche n'est pas claire car tu ne peux pas "enlever" ainsi $x^2$ de chaque côté.
Cela revient à diviser chaque membre par $x^2$ mais dans ce cas , il faut diviser $16x$ par $x^2$, ce que tu n'as pas fait.

Le plus simple est de factoriser.

$2\pi x^2-16x=0$

Comme je te l'ai indiqué, mets 2x en facteur, ce qui donne

$2x(\pi x-8)=0$

Pour qu'un produit de facteurs soit nul il faut et il suffit qu'un des facteurs soit nul

1er cas : $2x=0$ <=> $x=0$
ce cas n'est pas acceptable car l'énoncé précise $x>0$

2ème cas : $\pi x-8=0$

d'où $x=...$

Donne ta réponse pour vérification si tu le souhaites.

[mtschoon]

@Smile-Shadow

SI tu souhaites utiliser ta méthode en "enlevant" $x^2$ comme tu as voulu le faire, je t'indique ce que tu peux faire.

Vu que $x>0$, $x$ ne peut pas prendre la valeur 0 donc $x^2$ non plus.
Tu peux donc diviser chaque membre de l'équation par $x^2$

$\pi x^2=16x-\pi x^2$

$\pi =\frac{16x}{x^2}-\pi$

En simplifiant :

$\pi =\frac{16}{x}-\pi$

En transposant $-\pi$ à droite :

$\pi +\pi =\frac{16}{x}$

$2\pi =\frac{16}{x}$

$2\pi x=16$

D'où $x=....$

Tu termines et tu dois trouver la même réponse qu'avec la méthode par factorisation.

[mtschoon]

@Smile-Shadow , bonjour,

J'espère que tu as trouvé $x=\frac{8}{\pi }$

Bon travail.