Fonction rationnelle mo

Bonjour !
Bon voilà je vous explique,
J’ai un dm à rendre mais je n’y arrive pas donc
pour la première fois je me suis dis que je vous demander de l’aide...
J’ai une fonction rationnelle tel que :
f(x)= (x^2+mx-2) / (x-m) définie sur ]m;+ l’inf.[
Je dois déterminer l’ensemble des valeurs de m pour que la fonction f ne soit pas strictement monotone

Merci d’avoir pris le temps de lire mon message
Heelpp meee.

@ElMatdorDelMar , bonjour,

Idée,

f est définie, dérivable (donc continue) sur ]m, $+∞+\infty$ [, vu que sur cet intervalle, le dénominateur ne s'annule pas.

f n'est pas strictement monotone , c'est à dire la dérivée f' n'est pas de signe constant, c'est à dire la dérivée f' s'annule.

Tu dois donc calculer $f^{'} (x)$

Ensuite, tu cherches pour quelles valeurs de m la dérivée peut s'annuler ( sur ]m, $+∞+\infty$ [ )

@mtschoon
Merci beaucoup ^^
J’ai déjà fini l’exercice, mais
c’est sympa de m’avoir répondu.
En effet on calcule f’(x)
puis avec les coefficient

a = 1 b= -2m et c = -m^2 +2 on calcul Delta,
Ce qui nous ramène à une équation du 2nd degré
8m^2 - 8
On recalcule Delta avec a = 8 b = 0 et c = -8
On a 2 racine x1 = -1 et x2 = 1 voilà voilà
Je dis ça pour les autres qui tomberont peut être sur cet exercice .

Sinon bonne journée.

@ElMatdorDelMar

Je pense que tu as trouvé

$f′(x)=x2−2mx−m2+2(x−m)2f'(x)=\dfrac{x^2-2mx-m^2+2}{(x-m)^2}$

Le signe de f'(x) est donc le signe de $x^2-2mx-m^2+2$

$Δ=8m2−8\Delta=8m^2-8$

$Δ\Delta$ s'annule pour $m_1=1$ et pour $m_2=-1$

J'espère que tu as tiré une bonne conclusion...(je l'ignore vu que tu ne la donnes pas )

@mtschoon
Si si ne vous inquiétez pas, la voici :
m sur l’interv [ -1 ; 1] le numérateur de la dérivée ne s’annule pas alors f est strictement croissante. Par analogie
m sur l’inter. ]-l’inf. ; -1 [u] 1; + l’inf. [ le numérateur s’annule alors f n’est pas strictement croissante.
En tout cas c’est ce qu’il me semble....

@mtschoon
Merci pour le temps que vous avez passé sur mon exercice !

@ElMatdorDelMar , de rien !

Si tu as bien détaillé tes explications sur $]m,+∞[]m,+\infty[$ , tes réponses sont exactes.

Bon travail !

est ce que tu peut m'aider pour la conclusion stp je galere...

@AlQa-holiq Bonjour, (Marque de politesse à ne pas oublier !!)

Analyse les éléments de réponse donnée et indique les points que tu ne comprends pas.

@AlQa-holiq , bonsoir,

@AlQa-holiq a dit dans Fonction rationnelle mo :

est ce que tu peut m'aider pour la conclusion stp je galere...

Je regarde ta question.

j'espère que tu as compris la démarche.

La condition d'existence de f (et de f') est $x≠mx\ne m$ (dénominateur non nul)
Donc sur $]m,+∞[]m,+\infty[$ f est définie, dérivable.

On travaille exclusivement sur l'intervalle $]m,+∞[]m,+\infty[$

$f′(x)=x2−2mx−m2+2(x−m)2f'(x)=\dfrac{x^2-2mx-m^2+2}{(x-m)^2}$

$(x−m)2>0(x-m)^2\gt 0$ donc $f^{'} (x)$ est du signe du numérateur $p(x)=x^2-2mx-m^2+2$

$p (x)$ est un polynôme du second degré dont le discriminant est $Δ=8m2−8=8(m2−1)\Delta=8m^2-8=8(m^2-1)$

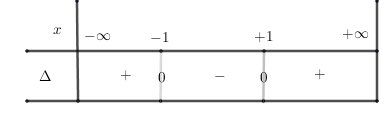
Les conclusions sont relatives au signe de $Δ\Delta$ .

1er cas : $m∈]−1,1[m\in]-1,1[$
$Δ<0\Delta \lt 0$ ; $p (x)$ est du signe du coefficient de $x^2$ c'est à dire 1, donc $p(x)>0p(x)\gt 0$ donc $f′(x)>0f'(x)\gt 0$ donc f strictement croissante sur $]m,+∞[]m,+\infty[$

2ème cas : $m = 1$ $Δ=0\Delta=0$
$p (x) = 0$ pour $x = 1$ et $p(x)>0p(x)\gt 0$ sur $]1,+∞[]1,+\infty[$
donc f strictement croissante sur $]1,+∞[]1,+\infty[$

3ème cas : $m = - 1$ $Δ=0\Delta=0$
$p (x) = 0$ pour $x = - 1$ et $p(x)>0p(x)\gt 0$ sur $]−1,+∞[]-1,+\infty[$
donc f strictement croissante sur $]−1,+∞[]-1,+\infty[$

4ème cas : $m∈]1,+∞[m\in]1,+\infty[$ , $Δ>0\Delta\gt 0$
$p (x) = 0$ pour $x1=2m+8m2−82=m+2m2−2x_1=\dfrac{2m+\sqrt{8m^2-8}}{2}=m+\sqrt{2m^2-2}$ et pour $x1=2m−8m2−82=m−2m2−2x_1=\dfrac{2m-\sqrt{8m^2-8}}{2}=m-\sqrt{2m^2-2}$

Sur $]m,+∞[]m,+\infty[$ , $p (x) = 0$ pour $x1=m+2m2−2x1=m+\sqrt{2m^2-2}$
Sur cet intervalle, pour $x<x1x\lt x_1$ , $p(x)<0p(x)\lt 0$ et pour $x>x1x\gt x_1$ , $p(x)>0p(x)\gt 0$ .
la dérivée change de signe donc f n'est pas strictement monotone.

5ème cas : $m∈]−∞,−1[m\in]-\infty, -1[$ , $Δ>0\Delta\gt 0$
Tu raisonnes comme pour le 4ème cas et même conclusion.

CONCLUSION GENERALE :
L’ensemble des valeurs de m pour que la fonction f n'est pas strictement monotone est donc :
$]−∞,−1[∪]1,+∞[\boxed{]-\infty,-1[ \cup ]1,+\infty[}$

Regarde tout ça de près si ça t'interesse.
Bonne lecture.

Bonjour, quelqu'un pourrait me détailler le calcul de la dérivée de f(x) parce que j'ai essayé plusieurs fois et je ne trouve pas comme vous. Merci d'avance

@Lucie-Boucheron , bonjour,

Pour le calcul de la dérivée, utilise la dérivée d'un quotient.

$U(x)=x^2+mx-2$
$U^{'} (x) = 2 x + m$
$V (x) = x - m$
$V^{'} (x) = 1$

$f′(x)=U′(x)V(x)−U(x)V′(x)(V(x))2f'(x)=\dfrac{U'(x)V(x)-U(x)V'(x)}{(V(x))^2}$

Bon calcul.

@Lucie-Boucheron , bonjour,

Si ça t'arrange, j'explicite le calcul de la dérivée, en appliquant les données que je t'ai indiquées.

$f′(x)=(2x+m)(x−m)−(x2+mx−2)(1)(x−m)2f'(x)=\dfrac{(2x+m)(x-m)-(x^2+mx-2)(1)}{(x-m)^2}$

Tu développes :
$f′(x)=2x2−2mx+mx−m2−x2−mx+2(x−m)2f'(x)=\dfrac{2x^2-2mx+mx-m^2-x^2-mx+2}{(x-m)^2}$

Tu simplifies le numérateur:
$f′(x)=x2−2mx−m2+2(x−m)2\boxed{f'(x)=\dfrac{x^2-2mx-m^2+2}{(x-m)^2}}$

CQFD