Situer une courbe et ses tangentes

Bonjour, j'aimerai avoir une autre méthode de résolution pour l'exercice suivant,

Dans un repère orthonormé, démontrer que la courbe représentative de la fonction ln est en dessous de chacune de ses tangentes.

Moi j'ai cherché à démontrer que la fonction ln est concave en utilisant la dérivée seconde mais je trouve que ça manque de rigueur, merci d'avance pour votre aide !

@mimims
Bonjour,
Ca ne manque pas vraiment de rigueur, car tu t'appuies sur un théorème de cours que tu as probablement déjà démontré en classe.

Néanmoins, si tu veux pousser un peu plus la réflexion, je te propose de comparer la position de la courbe représentative de la fonction $l n$ avec celle d'une tangente quelconque à cette courbe en une abscisse quelconque $a$ strictement positive.

Tu connais l'expression de la tangente à la courbe représentative d'une fonction $f$ en un point d'abscisse $a$ de son ensemble de définition ?

@Guillaume-87 Oui l'expression de la tangente à la courbe C représentative de la fonction f(x)=lnx en un point a est :

Ta : y =f'(a)(x-a)+f(a)

ta : y=(1/a)x-1+ln(a)

@mimims
Très bien, maintenant tu poses $D(x)=ln(x)−[(1/a)x−1+ln(a)]D(x)=ln(x)-\left[ (1/a)x-1+ln(a)\right]$ .
En étudiant son signe, tu obtiendras la position des deux courbes, c'est-à-dire la position de la courbe de la fonction $l n$ avec celle d'une tangente quelconque.

Connaissais-tu cette technique ?

@Guillaume-87 Ah oui ! On fait la différence entre la tangente et ln et si c'est positif c'est que T est au dessus de ln, merci infiniment pour votre aide !

@mimims
Pas de souci, c'est avec plaisir !

Tu verras, l'étude complète du signe de cette expression, une fois réduite et simplifiée, est intéressante car elle fait appel à toutes les notions d'analyse que tu as vues : dérivation, étude du signe de la dérivée, calcul des limites avec levée d'indétermination, et bien sûr beaucoup de calculs algébriques puisque $a$ ne peut pas être remplacée par une valeur connue et chiffrée. Il y a presque tout !

@Guillaume-87 Toutefois, comment dois-je procéder pour l'étude de signe ?

@mimims , Re-bonjour,

En attendant que @Guillaume-87 soit reconnecté, je te donne une piste pour ta dernière question.

$D(x)=lnx−1ax+1−lnaD(x)=lnx-\dfrac{1}{a}x+1-lna$ , avec $a>0a\gt 0$

Tu étudies le sens de variation de la fonction $D$ sur $]0,+∞[]0,+\infty[$ (de façon usuelle : dérivée, signe de la dérivée, ...)

Tu fais le tableau de variation , tu calcules le maximum de $D (x)$ et tu trouveras la conclusion souhaitée.

@mimims
Tout à fait, @mtschoon a raison sur la méthode, même si il y a une erreur de développement de l'expression de D(x) si je ne m'abuse (il y a un $l n$ en trop, après le $1a\frac{1}{a}$ ).
Merci en tout cas !

@Guillaume-87 , de rien

Exact, je viens de supprimer ce $l n$ indésirable, merci !

@mimims Re-bonjour,

Si tu veux vérifier le tableau de variations qui te permettra de conclure, en voici un :

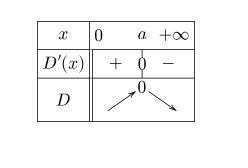
(Je n'ai pas indiqué les limites, car vu le but, elles ne sont pas nécessaires)

@mtschoon Merci bien pour votre aide !

De rien @mimims et bon travail !

@mimims Bonjour
Pourrais-je avoir l'intégralité de ton exercice stp?