Exercice Mathématique 4ème les équations
-
Black Storm dernière édition par

Bonjour, que vaudra x si on a :
x carré-x=-1
Merci d'avance
-
Bonjour Black-Storm,
L'énoncé est-il correct ?
x2−x=−1x^2 -x = -1x2−x=−1Comment résous-tu les équations du second degré ?
par factorisation ?
-
mtschoon dernière édition par mtschoon

Bonjour,
@Black-Storm , ta question ne correspond pas au programme de quatrième français...
Ou bien tu t'es trompé de rubrique ou bien tu appliques un programme autre que français.
Par exemple, je viens de constater qu'en Belgique, fontion polynôme du second degré et équation du second degré font partie du programme de 4ème.
Un(e) modérateur(trice) pourra déplacer la question (en modifiant le titre), pour la mettre dans la rubrique adaptée.
Des possibilités usuelles pour résoudre ;
Par exemple, avec la fonction f définie par f(x)=x2−xf(x)=x^2-xf(x)=x2−x
f(x) est de la forme f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c avec a=1,b=−1,c=0a=1, b=-1, c=0a=1,b=−1,c=0
le minimum est obtenu pour x=−b2a=12x=\dfrac{-b}{2a}=\dfrac{1}{2}x=2a−b=21
Après calculs, f(12)=−14f(\dfrac{1}{2})=-\dfrac{1}{4}f(21)=−41donc , pour tout x réel, f(x)≥−14f(x)\ge \dfrac{-1}{4}f(x)≥4−1
Conclusion :
il n'existe aucune valeur de x réelle telle que x2−x=−1x^2-x=-1x2−x=−1Illustration graphique :
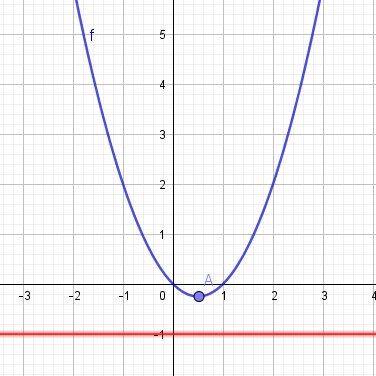
Autre façon , par résolution d'une équation du second degré.
de la forme ax2+bx+c=0ax^2+bx+c=0ax2+bx+c=0
x2−x=−1x^2-x=-1x2−x=−1 <=> x2−x+1=0x^2-x+1=0x2−x+1=0
Tu cherches le discriminant Δ\DeltaΔ que tu dois trouver strictement négatif, d'où la réponse.Tiens nous au courant si besoin.