Fonctions et Limites - TS

Bonjour on est en train de commencer le cours des Limites des fonctions et le prof nous a déjà envoyée des exercices, merci déjà pour l'aide!

Soit l'équation (E) 𝑥3−5𝑥=3.1.

Démontrer que l'équation (E) admet une unique solution sur l'intervalle [-1; 0].
On souhaite obtenir un encadrement d'amplitude 10−2de cette solution. Après avoir analysé l'algorithme ci-dessous, compléter les pointillés de façon à résoudre le problème![Sin títulomaths.png]
(/assets/uploads/files/1586962335376-sin-títulomaths.png)

3.L'équation (E) admet-elle des solutions n'appartenant pas à [-1; 0]? Justifier. Si oui, pour chaque solution, modifier l'algorithme précédent de façon à en obtenir un encadrement d'amplitude 10−2.

@Mateo-S Vous pouvez visualiser l'image?

@Mateo-S @mtschoon

Bonjour Mateo-S,

L'image de l'algorithme n'est pas visible.

Bonjour,

@Mateo-S , pour la question 2), écris donc l'algorithme "à la main".
En principe, ici, c'est ce qu'il faut faire vu que seuls les scans de graphiques et tableaux sont autorisés.

Tu peux déjà commencer par traiter la question 1 avec le TVI

Je suppose que tu as voulu écrire : $x^3-5x=3.1$

Je te conseille d'étudier la fonction f définie par $f(x)=x^3-x$ sur R pour pouvoir répondre à la question 1) et au début de la question 3).

Pour vérification, je t'indique le tableau de variations que tu dois trouver mais je ne mets aucun des calculs utiles.
(je n'ai pas non plus calculé le minimum et maximum relatifs)
Si tu ne trouves pas , demande.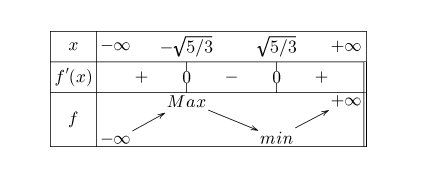

Conséquence :
[-1,0] est inclus (strictement) dans $]−5/3,5/3[]-\sqrt {5/3},\sqrt{5/3}[$
Donc, sur [-1,0], f est définie, dérivable donc continue et strictement décroissante, donc bijective de [-1,0] vers [f(0), f(-1)]
Tu calcules f(-1) et f(0) et tu pourras répondre, avec le TVI , à la question 1)

Tiens nous au courant.